Ascomp.ch

Direct Numerical Simulation
of Turbulent Heat Transfer Across
a Mobile, Sheared Gas-Liquid
Interface
The impact of interfacial dynamics on turbulent heat transfer at a deformable, shearedgas-liquid interface is studied using Direct Numerical Simulation (DNS). The flow system comprises a gas and a liquid phase flowing in opposite directions. The governing equa-tions for the two fluids are alternately solved in separate domains and then coupled at the M. Fulgosi
interface by imposing continuity of velocity and stress. The deformations of the interfacefall in the range of capillary waves of waveslope ak⫽0.01 (wave amplitude a times wavenumber k), and very small phase speed-to-friction velocity ratio, c/u . The influence of low-to-moderate molecular Prandtl numbers 共 Pr兲 on the transport in the immediatevicinity of the interface is examined for the gas phase, and results are compared to Institute of Energy Technology, existing wall-bounded flow data. The shear-based Reynolds number Re is 171 and Swiss Federal Institute of Technology, Prandtl numbers of 1, 5, and 10 were studied. The effects induced by changes in Pr in ETH-Zentrum/CLT, CH-8092 Zurich, both wall-bounded flow and over a gas-liquid interface were analyzed by comparing the relevant statistical flow properties, including the budgets for the temperature variance andthe turbulent heat fluxes. Overall, Pr was found to affect the results in very much the S. Banerjee
same way as in most of the available wall flow data. The intensity of the averaged normalheat flux at high Prandtl numbers is found to be slightly greater near the interface than at Department of Chemical Engineering, the wall. Similar to what is observed in wall flows, for Pr⫽1 the turbulent viscosity and University of California, diffusivity are found to asymptote with z⫹3, where z⫹ is the distance to the interface, and Santa Barbara, CA 93106, USA with z⫹n, where n⬎3 for Pr⫽5 and 10. This implies that the gas phase perceivesdeformable interfaces as impermeable walls for small amplitude waves with wavelengthsmuch larger than the diffusive sublayers. Moreover, high-frequency fluctuating fields areshown to play a minor role in transferring heat across the interface, with a markedfiltering effect of Pr. A new scaling law for the normalized heat transfer coefficient, K⫹has been derived with the help of the DNS data. This law, which could be used in therange of Pr⫽1 to 10 for similar flow conditions, suggests an approximate Pr⫺3/5 rela-tionship, lying between the Pr⫺1/2 dependence for free surfaces and the Pr⫺2/3 law forimmobile interfaces and much higher Prandtl numbers. A close inspection of the transferrates reveals a strong and consistent relationship between K⫹, the frequency of sweepsimpacting the interface, the interfacial velocity streaks, and the interfacial shear stress. Keywords: Heat Transfer, Turbulence, Two-Phase, Interface coefficient with the Reynolds and Prandtl/Schmidt numbers. Theprinciple consists in relating local mass transfer rates and scalar Most investigations dealing with turbulent heat and mass trans- fluxes to the properties of the fluctuating velocity field. The clas- fer have traditionally focused on simple configurations involving sical approach uses the analogy between diffusion of momentum rigid or flat surfaces. In practice, however, single-phase or two- and of a scalar quantity 共heat or mass兲, extending Fick's gradient phase flows may take place in the presence of boundaries which laws up to the turbulent regime, i.e., the scalar turbulent diffusiv- are neither flat nor rigid. In multi-phase flow systems involving ity, ␣t , is made proportional to the turbulent viscosity, ␯t . The immiscible fluids, the interface separating the fluids plays a role surface renewal theory 关3兴 has also been widely employed to pa- similar to that of an impermeable boundary. An example is the rametrize gas-liquid mass transfer rates. Its principle consists in exchanges between the atmosphere and the oceans taking place relating the mass transfer rate to the time between sweeps and across a continuously deforming interface. On a much smaller bursts (␶ren) impinging on the interface, assumed to be responsible scale, gas-liquid exchange mechanisms across deformable inter- for surface renewal, i.e., K⬅(D/␶ren)1/2, where D⫽␯/Pr refers to faces may be encountered in annular flows, falling liquid films, molecular diffusivity of heat 共or mass by simply replacing Pr with Sc, the Schmidt number兲.
Environmental studies on CO2 absorption by the oceans 关1,2兴 Heat and mass transfer at interfaces depends on the resistance have focused on the proper scaling of the averaged mass transfer of diffusive layers with thickness ␦ ⬃ O (0.01 mm) on the liquid O (1 mm) on the gas side. Accordingly the transport †To whom correspondence should be sent. E-mail: [email protected]; across both layers is controlled by fine-scale turbulence, so that Phone: ⫹4116324613 the transport mechanisms can be faithfully simulated only by the Contributed by the Heat Transfer Division for publication in the JOURNAL OF use of DNS. The complexity of the problems increases if the HEAT TRANSFER. Manuscript received by the Heat Transfer Division July 17, 2002;revision received June 18, 2003. Associate Editor: K. S. Ball.
interface is further sheared and free to deform, in which case an Journal of Heat Transfer
Copyright 2003 by ASME
DECEMBER 2003, Vol. 125 Õ 1129

extra transverse motion superimposed on the mean flow is ex- eddy diffusivity. Moreover, a scaling law for the heat transfer pected to occur in the direction normal to the interface. The con- coefficient based on the effective viscous friction velocity is tinuously deformable interface could then affect the heat/mass transport indirectly by modifying the turbulence in the vicinity ofthe interface, or more precisely by increasing the portion of fric-tional drag transferred into form drag. The importance of such Mathematical Model and Numerical Strategy
phenomenon is not yet clear, but a higher impact is expected if the The configuration of the problem is sketched in Fig. 1. The surface is populated by capillary waves with wavelengths up to an streamwise direction is denoted by x, the spanwise direction by y order of magnitude larger than ␦G . For longer waves, the time and the interface-normal 共gravity兲 direction is referred to as z. The scale over which the surface renews its structure becomes too two phases are flowing counter-currently and are separated by an large compared to the turbulence time scale, and the movement of interface free to deform in three dimensions.
the interface does not affect the transport phenomena. In sum-mary, momentum and heat/mass transfer across deformable, The gas and liquid phases 共des- sheared interfaces depends on the nature of the waves, and hence ignated by the subscripts G and L, respectively兲 are considered as on the interfacial shear inducing them. An important question that Newtonian and incompressible fluids, flowing in separate do- arises then is whether the interfacial heat transfer scales with the mains, and driven by an imposed constant mean pressure gradient.
friction velocity based on frictional drag and kinematic viscosity.
The reference quantities employed for normalization in each do- Although confined to simple configurations involving flat and main are the effective shear velocity u ⫽冑␶ int / ␳ , where ␶ int is the non-deformable interfaces, early DNS studies proved particularly viscous interfacial shear stress, the half-depth of each computa- efficient in providing insight into the scalar exchanges all the way tional domain h, and the kinematic viscosity ␯. It is important to down to the diffusive sublayer. The contributions have generally note that, at the beginning of the simulation when the interface is concentrated on two aspects: a first group essentially focused on flat, the viscous interfacial shear stress balances exactly the mean modeling turbulent convection mechanisms 关4 –7兴, while a second pressure gradient driving the flow, and u corresponds to the dealt with mass transfer 关8,9兴. Wall flow simulations at similar shear velocity u␶ . As the waves start to form and develop, part of Reynolds numbers, but for different thermal boundary conditions, the energy is transferred into form drag, so that u ⬍u produced DNS data for the development and calibration of turbu- The reference temperature T lent scalar convection models. The studies involving heat andmass transfer are the most relevant ones for the present contribu- tion. Campbell and Hanratty 关8兴, who pioneered this class of q ⫽⫺␭冉 dT¯ DNS, were interested in identifying the frequency fluctuations controlling most of the transfer at the wall. McCready et al. 关9兴re-investigated the problem considering a flat, mobile gas-liquid where qint represents the interfacial heat flux. The time is made interface. Lyons et al. 关6兴 simulated the case of differential heating nondimensional using ␯/u , and the length scales are normalized between channel walls. Calmet and Magnaudet 关10兴 showed that using u /␯. In each computational domain, the shear Reynolds similar results can be obtained for Sc⫽200 by use of LES, sup- number is defined as Re ⫽u 2h/␯.
porting the fact that the effect of high-frequency turbulence near With the reference quantities defined above, the Navier-Stokes the wall is filtered out by increasing Pr or Sc 关9兴. Na et al. 关7兴 and energy equations governing the flow in each domain can be studied the effect of the Prandtl number on turbulent statistics written in nondimensional form as characterizing transport and the spatial variation of the variance ofthe fluctuating temperature. The very recent contribution of Piller et al. 关11兴 examines the influence of low Prandtl numbers 共0.025–1.0兲 on turbulent transport in channel flow. Their study has shown the molecular conductivity to act as a filter for high-frequency velocity fluctuations as Pr decreases, rendering them ineffective in the heat exchange processes.
Paralleling these studies, new results have been obtained in this area with the appearance of DNS of turbulent flows over wavy walls and sheared, gas-liquid interfaces 关12–14兴. Lombardi et al.
关12兴 performed a DNS of coupled gas-liquid flows over a flat where u⫹⫽(u⫹,v⫹,w⫹) is the nondimensional 共by u ) velocity
interface, which revealed that the interface appears to the gas phase almost like a rigid wall, whereas the liquid perceives the vector, p⫹ is the dynamic pressure normalized by ␳u , T⫹ is the interface like a slip surface. De Angelis et al. 关13兴 studied flows nondimensional temperature defined as T⫹⫽(T⫺Tint)/T , and over rigid, sinusoidal wave trains. Their results show that fixed, is the mean bulk velocity. The last term in Eq. 共4兲 is the high-amplitude waves exert significant effects on the mean flow source term needed to accurately predict the scalar transfer rate at and turbulence characteristics. De Angelis et al. 关14兴 employed low Prandtl numbers 关4兴. The conventional notation the same tools to study turbulent mass transfer at the sheared anddeformable gas-liquid interface in the limit of capillary waves. A detailed comparison of the turbulence structure at the two differ-ent types of interface has been provided by Fulgosi et al. 关15兴.
The objective of the present study is to complement the afore- mentioned contributions by exploring the heat transfer processesat a deformable interface, separating counter-flowing gas and liq-uid. The emphasis is on wave-induced mechanisms influencingthe flow and the associated heat transfer in the context of low-to-moderate Pr numbers. The analysis is limited to the gas side, dueto the presumed similarity between near-wall and near-interfaceturbulence. The effect of Prandtl number 共Pr⫽1, 5 and 10兲 on thethermal field is investigated by means of a global analysis of theaveraged heat fluxes, u ␪ , the temperature variance, ␪2, and the Geometry of the simulated two-phase flow
1130 Õ Vol. 125, DECEMBER 2003
Transactions of the ASME
is adopted to decompose the velocity and temperature fields intomean and fluctuating 共turbulent兲 components.
In the absence of phase change, the gas and liquid phases are coupled at the interface by the con-tinuity conditions for normal and shear stresses, velocity and tem-perature 共see, for example, Delhaye 关16兴兲, i.e., Energy spectra at z¿Ä5 for the velocity components, in
the gas phase: „a… streamwise direction; and „b… spanwise di-
rection.
where ␴⫹ is the viscous stress tensor, f ⫹ is a measure of the
vertical displacement of the interface with respect to the mid
plane, n and ti are the normal and the two tangential unit vectors,
respectively, and R⫽冑␳L /␳G is the density ratio parameter. The
Weber 共We兲 and Froude 共Fr兲 numbers are defined as
The convective term is explicit, with J⫽2, ␤ ⫽ ⫽⫺1/2, as in the Adams-Bashforth 共AB兲 scheme. The viscous term is implicit and discretized using the Crank-Nicholson 共CN兲 semi-implicit scheme. The time marching is second-order accurate gh共␳ ⫺␳ 兲 in the computation of the intermediate velocity uˆ, the value of
which is corrected in the next step using
where ␥ is the surface tension.
The interface motion is simulated by solving a pure advection equation for the vertical elevation of the interface, f (x,t), written
in nondimensional form as The unknown pressure field pn⫹1 can be obtained by taking the divergence of Eq. 共11兲 which, using the condition that un⫹1 is
⳵ ⫹u •ⵜ f ⫹⫽0
solenoidal, results in the Poisson equation The approach based on advecting Eq. 共9兲 and solving for the gas and the liquid fields separately is a boundary fitting method. In contrast to interface tracking methods, this approach cannot beextended to strong topological changes of the interface that mightlead to the inclusion of one phase into the other, such as fragmen- The energy Eq. 共4兲 is also solved using a second-order accurate tation and wave breaking 关17兴.
time differencing Periodic boundary conditions are applied in the streamwise 共x兲 and spanwise 共y兲 directions. At the outer boundaries, symmetry boundary conditions are employed for the thermal field, whereas free-slip boundary conditions are imposed on the velocity field.
The governing equations are solved using a collocation pseudo-spectral technique employing where the explicit (J⫽2, ␦ ⫽ 1/2) convective term Fourier series in the homogeneous, streamwise and spanwise di- is discretized using the AB scheme, and the implicit diffusive term rections, and Chebychev polynomials in the non-uniform direction is discretized by use of the CN scheme.
normal to the interface. The physical domain is mapped into a The size of each computational domain is 4␲h⫻2␲h⫻2h in rectangular parallelepiped at each time step. Equations 共2兲, 共3兲, streamwise, spanwise and interface-normal directions, corre- and 共4兲 are first solved separately in each domain, then coupled at sponding to 1074⫻537⫻171 wall units. As capillary waves do not the interface 共identified by solving Eq. 共9兲兲 through the continuity produce significant domain distortion, a grid resolution 共for each conditions 共7兲: on the gas side, the interfacial conditions apply to domain兲 of 64⫻64⫻65 in the streamwise, spanwise and interface- velocities and the temperature, whereas on the liquid side they normal directions was found to be appropriate for the solution of apply to stresses and the temperature. Procedures for de-aliasing the isothermal flow field. This is proved in Fig. 2, displaying the the solutions based on the two-thirds rule apply in this context, energy spectra against wave numbers kx and ky for the three ve- locity components, evaluated at a distance of five wall units from A modified version of the two-step fractional time splitting the interface, in the gas side. The result shows no energy accumu- method introduced by Temam 关18兴 is employed. In the first step, lation at high wave numbers, confirming that this resolution is an intermediate value for the velocity uˆ is determined by solving
sufficiently accurate for the solution of the velocity field. The the momentum equation, without the pressure gradient term extension of the spectrum to higher wave numbers, obtained bydoubling the grid resolution in the interface-normal direction, did not show energy accumulation either 共result not presented here兲.
In their review of past DNS of heat transfer in channel flow, Piller et al. 关11兴 note that the differences observed between some of the Journal of Heat Transfer
DECEMBER 2003, Vol. 125 Õ 1131
Grid points in each domain 0.024 ␯/u2 0.012 ␯/u2 0.012 ␯/u2 published results were chiefly due to insufficient statistical con-vergence, rather than to lower space resolution in the wall-normaldirection.
Saturation spectra of the wave fields at the beginning
and at the end „Bout of the sampling period
The shear Reynolds number Re each phase equal to 171. The inter-phase heat transfer does notinclude phase change. To limit the wave amplitude and steepnessto the range of capillary waves, the Weber and Froude numbers consideration here, this averaging procedure can be reliable only were set equal to We⫽4.8⫻10⫺3 and Fr⫽8.7⫻10⫺5. The gas if the collected data cover a sufficiently large time interval over and liquid phases considered are such that R⫽29.9. Three differ- which the wave properties do not change. The statistical station- ent thermal conditions have been investigated, namely Pr⫽1, 5 arity of the wave field is discussed below.
and 10. For Pr⫽1, the spatial resolution employed in each domainis 64⫻64⫻65 共hereinafter referred to as G1兲, whereas for Pr⫽5 Characteristics of the Waves.
The topology of the and 10, it was doubled in the direction normal to the interface, i.e.
waves developing over a deformable free surface takes various 64⫻64⫻129 共referred to as G2兲. The grid resolutions in G1 forms, depending on the intensity of the interfacial shear stress (⌬x⫹⫽16.77, ⌬y⫹⫽8.38, ⌬z⫹⫽0.102⫺4.191) and G2 (⌬x⫹ caused by the nature of the underlying turbulence. The action of ⫽16.77, ⌬y⫹⫽8.38, ⌬z⫹⫽0.026⫺2.096) are comparable to this shear is balanced by two stabilizing factors: one due to grav- those employed by Tiselj et al. 关19兴. The time increments are ity and one caused by surface tension. The specialized literature 0.024 ␯/u2 for the G1 grid, and 0.012 ␯/u2 for G2.
20兴 characterizes the wave field in terms of saturation spectrum After statistically stationary conditions were achieved in each run, the velocity and thermal fields were collected over 4000␯/u2 nondimensional time units. The criterion used to establish steady state conditions was that the turbulent shear stress, u⫹w⫹, and theturbulent heat flux, w⫹␪⫹, were no longer varying over a time in which ⌿ is the two-dimensional wave spectrum, and Z(r) is the
interval of 1000 nondimensional time units. The simulation pa- covariance of the instantaneous nondimensional surface displace- rameters are summarized in Table 1.
Interpretation of Results
Motivated by the uncertainties as to the existence of a similarity It is important to observe that, since the wavelength k is here between near-wall and near-interfacial turbulence, Fulgosi et al.
defined in the dimensional space, ⌿ has the dimension of 关L2兴, so 关15兴 studied the turbulent gas flow over the deformable interface, that a coefficient k2 is needed in the definition of the saturation and compared the results to wall-bounded flow data at the same spectrum 共14兲. The reader is referred to Phillips 关20兴 for further shear Reynolds number. In a time-averaged sense, the interfacial theoretical details. The wave saturation spectra, obtained using motion was seen to affect some features of the turbulence field in grid G1, are plotted in Fig. 3 at two different times during the the near-interface region; the most pertinent effect is a general simulation: at the early stage 共referred to as B dampening of the turbulent fluctuating field which, in turn, leads in in Fig. 3兲 and at the end 共referred to as B to a reduction in the interfacial dissipation. Furthermore, the tur- out) of the time interval over which the statistical analysis has been performed. The graph clearly indi- bulence was found to be less anisotropic at the interface than at cates that the wave properties did not change significantly within the wall. The analysis of the turbulent kinetic energy and Rey- this time interval, confirming the existence of the saturation or nolds stress budgets revealed that the interface deformations equilibrium range, which is synonymous to convergence in this mainly affect the so-called boundary term involving the redistri- context. The impact of the interfacial motion can then be inferred bution of energy, and the dissipation terms, leaving the production in an average sense.
terms almost unchanged. Away from the interface, the decompo-sition of the fluctuating velocity gradient tensor demonstrated that Statistics of the Thermal Field.
The mean temperature the fluctuating rate-of-strain and rate-of-rotation at the interface profiles plotted against the distance to the interface are shown in influence the flow throughout the boundary layer more vigorously.
Fig. 4共a兲 for all Prandtl numbers. The results obtained by Kawa- Following this comparative strategy, in the present work, the mura et al. 关5兴 at Re␶⫽180 for Pr⫽1 and Pr⫽5, and by Tiselj interfacial turbulent heat transfer in the gas is investigated, and the et al. 关21兴 at Re␶⫽171 for Pr⫽1 and Pr⫽5.4 共for an isothermal results compared to wall-bounded flow data to reveal the effect of wall boundary condition兲 have been included for comparison. For the interfacial deformation on heat transfer mechanisms for a Pr⫽10 the present DNS has been compared to that of Na et al. 关7兴 range of low Prandtl numbers. As it is customary in DNS, the at Re␶⫽150. For Pr⫽1 the present results agree fairly well with statistical analysis of the data is performed by averaging the col- both databases 关5,21兴, whereas for Pr⫽5 the agreement is better lected velocity and thermal database over the two homogeneous with the data of Kawamura et al. 关5兴 than with those of Tiselj directions 共i.e., x-y plane average兲 and in time. For the flow under et al. 关21兴. For Pr⫽10 the comparison with the data of Na et al.
1132 Õ Vol. 125, DECEMBER 2003
Transactions of the ASME
Root mean square value of temperature fluctuations.
Lines are used to identify the present DNS result:
, PrÄ5; -"-"-, PrÄ10. Symbols identify respectively: ¿,
PrÄ1 and Ã, PrÄ5: DNS of Kawamura et al. †5‡; 䊊, PrÄ1 and 䊐,
PrÄ5: DNS of Tiselj et al. †21‡; 䉭, PrÄ10: DNS of Na et al. †7‡.
towards the boundary. Both the present results and those of Kawa-mura et al. 关5兴 for Pr⫽1, the maximum of the temperature fluc-tuations is located around z⫹⫽17. Increasing the Prandtl numberto 5 shifts the peak location to about z⫹⫽7 in the wall-boundedflow, and to around z⫹⫽9 in the flow over the deformable inter-face. The wall flow data of Na et al. 关7兴 show the maximum of thetemperature fluctuations located around z⫹⫽3, whereas thepresent study shows that location to be around z⫹⫽5. It is inter-esting to note that the exact location of the maximum r.m.s. value Mean temperature profiles. „a… Comparison with other
DNS databases. Lines are used to identify the present DNS re-
is not correlated with the position of the edge of the diffusive , PrÄ5; -"-"-, PrÄ10. Symbols identify
␪ : the two locations tend to coincide with increasing respectively: ¿, PrÄ1 and Ã, PrÄ5: DNS of Kawamura et al. †5‡;
Prandtl number.
䊊, PrÄ1 and 䊐, PrÄ5: DNS of Tiselj et al. †21‡; 䉭, PrÄ10: DNS
The first important conclusion to be drawn from the above com- of Na et al. †7‡. „b… Present DNS extrapolated data; lines are
parisons is that, as in wall flows, the most relevant statistical used to identify present DNS results and symbols to identify
quantities scale with the friction velocity, based on frictional drag.
the fitting equations.
The ratio of frictional drag to total drag 共including form drag兲 wasfound to be around 0.98. The second important finding is the appreciable effect of Pr on ␪⫹2, indicating that the range of wave 关7兴 is overall satisfactory. Figure 4共b兲 shows that inside the diffu- numbers in the thermal fluctuating field increases with Pr, for sive sublayer, the mean temperature profiles are in agreement with which the spectral functions of the velocity field are negligible.
the linear relation ⌰⫹⫽Pr.Z⫹.
Further analysis of the data also permits to identify the extent of Turbulent Fluxes and Inter-Phase Heat Exchange.
the logarithmic layer, where ⌰⫹⫽1/␬ Figure 6 shows the nondimensional averaged turbulent heat flux ␪ ln z⫹⫹B␪ . Both the slope, ␪ , and the shift, B␪ , are found to vary with Prandtl number, THF兲, u⫹␪⫹, in the streamwise direction versus the dimension- though without leading to the establishment of a clear relation- less distance to the interface/wall. The data are compared to the ship. The diffusive sublayer exists in all three flows, with thick- wall-bounded flow DNS of Kawamura et al. 关5兴. For Pr⫽1 the streamwise THF over the deformable interface compares very ␪ decreasing with increasing Prandtl number, i.e., ⌬␪ ⬇6, 4 and 2 wall units, respectively, for Pr⫽1, 5 and 10. Whilethe results for ⌬⫹ ␪ agree with those of Na et al. 关7兴 and Kawamura et al. 关5兴, those for the slope and the shift deviate appreciablyfrom the data of Na et al. 关7兴. These deviations are perhaps due tothe lower Reynolds number used by Na et al. 关7兴 rather than thewall boundary conditions employed in their simulation. The dif-ference in the slopes, in particular, suggests that the intensity ofturbulence in 关7兴 is simply weaker.
The behavior of the fluctuating temperature field near the wall/ interface is generally accepted as a good indicator of the wayscalar turbulent transport operates. An important feature requiringunderstanding is the effect of the Prandtl number on the interplaybetween molecular and turbulent transport near the wall. Ther.m.s. values of the temperature fluctuations are presented in Fig.
5, where the results of Kawamura et al. 关5兴 and Tiselj et al. 关21兴for Pr⫽1 and Pr⫽5, and those of Na et al. 关7兴 for Pr⫽10, areagain included for comparison. As can be observed, in both wall-bounded and interfacial flows, the increase in Prandtl number cor- Streamwise turbulent heat flux and comparison with
responds to a shift of the maximum of the temperature fluctuations Kawamura et al. †5‡
Journal of Heat Transfer
DECEMBER 2003, Vol. 125 Õ 1133
Heat transfer coefficient
wall than at the mobile interface. The differences between thestreamwise and vertical THFs will be explained more fully inSection 3.5, where the budget equations for the heat fluxes arecompared term by term.
The nondimensional heat transfer coefficient 共HTC兲 is defined Pr 共T¯ ⫺T¯ 兲 int dz ⫹ int Interface-normal turbulent heat flux: „a… boundary layer;
and „b… near interfaceÕwall region and comparison with Kawa-
mura et al. †5‡.
¯ top represents the mean temperature at the upper boundary of the gas domain 共in 关22兴, T ¯ top was taken at the center of the closed channel兲. Note, too, that K⫹ is normalized by the effectivefriction velocity associated with a frictional drag u ⫽0.98u The scaling of the heat transfer coefficient with the effective fric- well with the wall data; the behavior is similar and the peak value tional velocity u has so far shown that it scales with Pr⫺1/2 at in both cases is located at the same distance from the interface/ mobile interfaces, and with Pr⫺2/3 at immobile interfaces 关9兴. De wall, z⫹⬇18, which corresponds to the location of the maximum Angelis et al. 关14兴 have shown the Pr⫺2/3 scaling to also hold on r.m.s. value of the temperature fluctuations. For Pr⫽5, the stream- the gas side of wavy gas-liquid interfaces, but for high-Sc num- wise THF near the interface exhibits some differences compared to that near the wall, but peak values are almost identical and are Figure 8 presents the values of the nondimensional HTC ob- furthermore reached almost at the same location from the tained for the gas side in the present DNS as a function of Prandtl interface/wall (z⫹⬇11). Beyond the peak location, however, the number. For the range of Pr investigated here, the present DNS THF for the flow over the deformable interface remains slightly provides the following variation of the HTC higher than for the wall flow. For Pr⫽10 the streamwise THFpeak location occurs at z⫹⬇8. This analysis confirms that increas-ing the molecular Prandtl number substantially increases the in- tensity of the heat flux when approaching the wall/interface, de-pending on the thickness of the thermal boundary layer. Awayfrom the diffusive thermal sublayer, the value of the THF drops which can be seen to vary between ⬀Pr⫺1/2 for free surfaces and faster for higher Prandtl numbers. Deeper in the bulk flow, heat ⬀Pr⫺2/3 for immobile interfaces for much higher Prandtl numbers.
transfer by turbulent transport does not depend much on the For instance, the DNS of Na et al. 关7兴 delivered smaller values for Prandtl number.
both the coefficient of proportionality and the exponent, i.e., Figure 7共a兲 presents the distribution of the nondimensional av- 0.0509 and 0.546, respectively. A parameterization of the scalar eraged THF in the direction normal to the interface, w⫹␪⫹. We transfer rate by reference to the surface renewal theory, using the note that, as the molecular Prandtl number increases, the peak above result, yields location moves closer to the interface, and so does the intensity ofthe flux. The differences between the near-interface and near-wall values 共at z⫹⬍10) of the normal THF are analyzed in detail in K⫹⫽0.41 ␶ Fig. 7共b兲. For both Pr⫽1 and Pr⫽5 the flux intensity near thedeformable interface is higher than at the wall. This implies that the interfacial dynamics leads to an increase in the vertical THF as where the normalized 共by ␯/u2 ) mean time between sweeps, ␶ compared to the situation near the rigid wall. The only plausible given by the DNS is approximately equal to f ⫺1 ⫽50, where explanation for this difference is that the waves promote the ve- f sweep denotes the frequency of sweeps ejections. Banerjee 关23兴 locity fluctuating field normal to the interface. Fulgosi et al. 关15兴 obtained a similar relationship for high-Sc mass transfer at solid indeed report that the turbulent kinetic energy decays faster at the walls based on the Leveque boundary layer solution, reading 1134 Õ Vol. 125, DECEMBER 2003
Transactions of the ASME

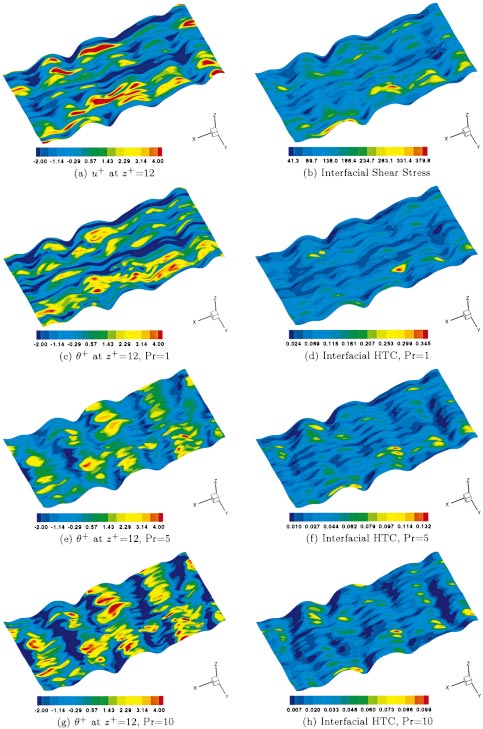
The elevation of the waves is amplified by factor 10: „a… u¿ at z¿Ä12; „b… interfacial
Shear Stress; „c… ␪¿ at z¿Ä12, PrÄ1; „d… interfacial HTC, PrÄ1; „e… ␪¿ at z¿Ä12, PrÄ5; „f…
interfacial HTC, PrÄ5; „g… ␪¿ at z¿Ä12, PrÄ10; and „h… interfacial HTC, PrÄ10.
K⫹⫽0.68 ␶⫹⫺0.5 Sc⫺0.66, ␪⫹ at z⫹⫽12, shown in the neighboring left panels 共Figs. 9共c兲, 9共e兲, 9共g兲兲. The comparison also includes contours of instanta- in which both the constant and the Sc power are actually functions neous velocity streaks, marked by contours of u⫹ at z⫹⫽12 共Fig.
of the Schmidt number. A close inspection of the Polhausens's 9共a兲兲, and of the instantaneous shear stress at the interface 共Fig.
boundary layer solution reveals on the other hand that the best fit 9共b兲兲. The three-dimensional interfacial waves can be seen to de- for Sc in the range of Pr⫽5 to 15 is obtained with the constant velop and propagate in the direction of the gas-flow 共in the pic- fixed to 0.6 and the Sc exponent to ⫺0.6.
tures the wave amplitude has been magnified by a factor ten兲.
Contours of the instantaneous HTC at the interface are shown Regions of high shear-high heat transfer rates at the crests can be in Figs. 9共d兲, 9共f兲, and 9共h兲, for Pr⫽1, 5 and 10, respectively, and clearly distinguished from regions of low shear-low heat transfer are compared with the thermal streaks represented by contours of rates at the troughs. The streaky structure of the velocity field is Journal of Heat Transfer
DECEMBER 2003, Vol. 125 Õ 1135
well represented by contours of u⫹, similar to what is observed inwall flow 关24兴, and is shown to conform to the thermal streaks forPr⫽1. This result indeed confirms the Reynolds analogy betweendiffusion of momentum and diffusion of heat; the deviations be-come evident with increasing Prandtl number.
Observing the HTC contours also reveals that heat transfer rates correlate with the interfacial shear; the largest values, occurring atthe bulges imposed by turbulent motions, correspond to stronglypositive shear values and positive u⫹ levels, presented in Fig.
9共a兲. According to the quadrant analysis of near-wall/interface tur-bulence structure 关12兴, this scenario is the signature of sweepevents through which the surface renews its structure, leading tohigh scalar transfer rates. By controlling surface renewal through-out the migration of high momentum fluid towards the interface,sweep motions create regions of high interfacial shear stress, lead-ing in turn to high heat transfer rates. The scalar transfer ratereaches its peak value when the sweep impinges on the surface;during the decay time the diffusive layer saturates by the actionsof molecular diffusion. On the other hand, increasing Pr producesa much finer thermal streaky structure and a decrease in heattransfer rate 共note that the scale of the plots changes with Pr兲.
As the turbulent kinetic energy represents an integral measure of the energy associated with thefluctuating velocity field, the variance of the fluctuating tempera-ture ␪2 may be regarded as the energy carried by the fluctuatingtemperature field. The equation for the evolution of the tempera-ture variance can be written in compact form 共see, for example,Nagano 关25兴兲 as D␪2 ⫽D where D/Dt is the substantial derivative. The first and secondterms on the right-hand side of this equation represent the diffu-sion by molecular actions and the diffusion due to turbulent trans-port, respectively. The third term is the production of ␪2 by theinteractions between heat fluxes and mean temperature gradients.
The last contribution represents the dissipation of the variance.
Figure 10 presents the budget terms obtained, for the gas side, from the present DNS. For the smaller Prandtl numbers, Pr⫽1 and5, results are again compared to the data of Kawamura et al. 关5兴.
For Pr⫽1, there are only small differences in the contributions tothe balance 共Fig. 10共a兲兲, which conforms with previous resultsregarding the thickness of the thermal and momentum boundary Budget for the temperature variance in the near
layers and averaged heat fluxes. The effects of interfacial motion interfaceÕwall region. Lines are used to identify the results of
on the fluctuating thermal field are negligible at this Prandtl num- the present DNS and symbols to identify the wall-bounded DNS
ber. As the molecular Prandtl number increases 共Fig. 10共b兲兲, minor results of Kawamura et al. †5‡. „a… PrÄ1; „b… PrÄ5; „c… PrÄ10.
deviations from the wall-bounded flow data begin to appear, inparticular concerning the production and turbulent diffusionterms. A comparison of the averaged normal heat fluxes in Fig.
7共b兲 explains why the production in wall flow is stronger than in the flow over the deformable interface.
The budget for Pr⫽10 presented in Fig. 10共c兲 indicates that the contribution of the production term becomes important with in- where the first term, P , represents the mean flow production due creasing Prandtl number, which is also true of the dissipation. In to the combined actions of mean temperature gradients and mean particular, these two contributions can be compared to the results velocity gradients. The second term is the pressure-temperature of Na et al. 关7兴 共their Figs. 7 and 13兲, which also show the values correlation, ⌸␪⬅⫺␪ⵜp. The third contribution, D␪ , designates of P␪ and ␧␪ at the wall to increase drastically for Pr⫽10. The the diffusive transport comprising molecular, Dm␪ , and turbulent behavior of the dissipation in the diffusive thermal sublayer ap- counterparts, Dt␪ . The last term, ␧␪ , refers to the dissipation of pears to be much more flat than for the case of the wall flow, and turbulent heat flux 共see, for example, Kasagi et al. 关4兴 or Nagano the starting value is also smaller.
关25兴 for the exact definition of each contribution兲.
Turbulent Heat Fluxes.
In turbulence modeling, the Budgets of the streamwise heat flux, u⫹␪⫹, for the gas flow most sophisticated approach accounting for the effects of data obtained by the present DNS were compared 共results not turbulence-induced stresses in the heat transport consists in solv- included here兲 to the channel-flow data of Kawamura et al. 关5兴, ing the transport equation for the turbulent heat fluxes, u ␪ for Pr⫽1 and 5. The comparison revealed the same behavior as than resorting to the eddy diffusivity concept. In compact form, observed before: the production becomes more important with this transport equation can be written as increasing Pr, the molecular diffusion dominates as a positive con- 1136 Õ Vol. 125, DECEMBER 2003
Transactions of the ASME
„a… Turbulent diffusivity; and „b… Turbulent diffusivity
in the vicinity of the deformable interface.
tion converges asymptotically almost to zero at z⫹⬇20. Forhigher Prandtl numbers, the sign of ␧␪ reverses exactly where the molecular and turbulent diffusion contributions change sign, too,indicating that in some flow regions the dissipation contributespositively as a gain. This was already revealed by Kasagi et al. 关4兴and Kawamura et al. 关5兴, and was attributed to the fact that thedissipation takes place in the large-scale structures.
Turbulent Thermal Diffusivity.
Turbulent thermal dif- fusivities were determined by averaging the thermal stress dataand temperature gradients in the homogeneous directions and intime. The turbulent thermal diffusivity, ␣t , was defined by apply-ing the simplified Gradient Diffusion Hypothesis 共GDH兲 Budget for the vertical turbulent heat flux in the near
interfaceÕwall region. Lines are used to identify the results of
the present DNS and symbols to identify the wall-bounded DNS
results of Kawamura et al. †5‡. „a… PrÄ1; „b… PrÄ5; „c… PrÄ10.
The impact of varying Pr on the distribution of eddy diffusivityscaled by Pr is shown in Fig. 12共a兲, where the eddy viscosity— tribution in the diffusive sublayer and is balanced by the dissipa- determined by use of GDH—is also included for comparison. For tion, while away from the wall/interface the production is bal- Pr⫽1 the data show the natural increase of ␣ anced by the dissipation. The behavior of the dissipation, ␧␪ , was t with distance to the interface, converging towards 15.5 at z⫹⫽100. An increasing particularly interesting: for Pr⫽1 its level gradually decreases Prandtl number has no effect on ␣ away from the wall/interface, whereas for Pr⫽5 and 10 it marks a t in the region close to the interface (z⫹⬍40), but a larger one away from it. The eddy dif- sharp drop at locations around the edge of the diffusive sublayer.
fusivity is shown to gain almost 30% in this flow region. An The effect of varying Prandtl number on the wall/interface- attempt to infer values of the turbulent Prandtl number from this normal heat flux balance, w⫹␪⫹, is discussed in relation to Fig.
plot would not be conclusive, owing to the ragged profiles of ␣ 11, comparing the wall and the present deformable interface da- the core flow region. Again, there is no clear picture on the exact tabases. Again, the production, which is negative in this case, dependence of ␣ gains in importance with increasing Pr, with the peak location t on Pr away from the interface.
The limiting behavior of the thermal diffusivity in the vicinity always moving closer to the wall. In contrast to the streamwise of the deformable interface is presented in Fig. 12共b兲, where the component, the production in the normal direction is balanced by turbulent diffusivity for momentum is also included. For Pr⫽1 the pressure-gradient correlation ⌸␪⬅⫺␪⳵ z p , and to a small ex- both ␣t and ␯t vary with z⫹3, as in wall flows. This again lends tent by the turbulent diffusion Dt␪ . The dissipation again shows support to the hypothesis that the interface appears to the lighter an interesting behavior: the peak value of ␧␪ in the diffusive su- phase like a wall. On the other hand, the result confirms the anal- blayer increases with the Prandtl number. For Pr⫽1 the dissipa- ogy between the diffusivities of momentum and heat for Pr⫽1.
Journal of Heat Transfer
DECEMBER 2003, Vol. 125 Õ 1137
However, at the same time it is noted that the slope of layer solutions. A close inspection of the transfer rates reveals a strong and consistent relationship between the transfer rate, the t / z ⫹n( n ⬎ 3 ) increases with Pr as the interface is approached.
This result suggests that ␣ ⬃ frequency of sweeps impacting the interface, the interfacial veloc- z⫹3 cannot be justifiably general- ized. The results of Na et al. 关7兴 reveal the existence of a conduc- ity streaks, and the interfacial shear stress. Similarly to what is tive layer at the wall, where ␣ observed in wall flows, for Pr⫽1 the turbulent viscosity/ t / z ⫹3 appears to be constant, al- though it is decreasing with increasing Pr.
diffusivity was found to asymptote with z⫹3. For higher Pr, how- In summary, deformable, sheared interfaces populated by cap- ever, the scaling was seen to change to z⫹n, with n⬎3. In the illary waves with small wavelength play a similar role in heat viscosity-affected layer the assumption that ␣ ⬃␯ t was found to transfer as solid walls. In particular, the near-interface limiting hold in this context, too, whereas in the outer core flow, ␣t was behavior is such that the normal velocity varies quadratically with greater than ␯t , and no clear picture emerged as to the distribution the distance to the interface, and therefore the shear stress u⫹w⫹ of the turbulent Prandtl number.
The present study has addressed only some of the many issues and the heat flux w⫹␪⫹ vary with z⫹3. The scaling for ␣t is, of this complex problem. It would be intriguing to see how statis- however, strongly tied to the Prandtl number, in that the variation tical quantities scale with higher imposed shear velocities, i.e., in with z⫹3 holds only for Pr⫽1. For Pr⫽5 and 10, on the other the presence of higher amplitude waves.
hand, the variation is proportional to z⫹n, where n⬎3.
The computations were performed on the NEC SX-5 at the Turbulent heat transfer across a mobile, sheared gas-liquid in- Swiss Center for Scientific Computing 共CSCS兲 in Manno, Swit- terface has been studied using direct numerical simulation. The zerland; in particular Marco Consoli is acknowledged for his help.
purpose of the investigation was to examine the impact of the Prof. A. Soldati, University of Udine, is gratefully acknowledged interfacial dynamics on turbulent heat transfer, and to investigate for his useful suggestions. The authors wish to thank Dr. V. De the influence of the Prandtl number on the transports by compar- Angelis, University of California, Santa Barbara, who made avail- ing the results to existing wall flow data. The motivation arose able the original isothermal version of the DNS code employed in from the fact that investigations dealing with turbulent scalar transfer have focused on simple configurations involving rigid,flat surfaces, while in multicomponent systems the flow necessar-ily involves interfaces that are neither flat nor rigid.
The flow system studied comprises counter-flowing gas and 关1兴 Komori, S., Nagaosa, R., and Murakami, Y., 1993, ‘‘Turbulence Structure and liquid phases, each at a shear-based Reynolds number of 171. The Mass Transfer Across a Sheared Air-Water Interface in Wind-Driven Turbu- interface deformations were limited to capillary-wave ripples with lence,'' J. Fluid Mech., 249, p. 161.
关2兴 Rashidi, M., Hetsroni, G., and Banerjee, S., 1992, ‘‘Wave-Turbulence Interac- waveslope ak⫽0.01. Since, for high density ratios, interfaces play tion in Free-Surface Channel Flows,'' Phys. Fluids A, 4, p. 2727.
a role similar to that of a solid boundary, emphasis has been 关3兴 Danckwerts, P. V., 1951, ‘‘Significance of Liquid Film Coefficients in Gas placed on the gas side. For both Pr⫽1 and Pr⫽5 the flux intensity Absorption,'' Ind. Eng. Chem., 43, p. 1460.
near the deformable interface was found to be higher than at the 4兴 Kasagi, N., Tomita, Y., and Kuroda, A., 1992, ‘‘Direct Numerical Simulation of Passive Scalar Field in a Turbulent Channel Flow,'' ASME J. Heat Transfer, wall. This implies that the interfacial dynamics leads to an in- 114, p. 598.
crease in the vertical THF as compared to its value near the rigid 关5兴 Kawamura, H., Ohsake, K., Abe, H., and Yamamoto, K., 1998, ‘‘DNS of wall. The explanation for this difference is that the waves enhance Turbulent Heat Transfer in Channel Flow With Low to Medium-High Prandtl the velocity fluctuating field normal to the interface, as was re- Number,'' Int. J. Heat Fluid Flow, 19, p. 482.
关6兴 Lyons, S. L., Hanratty, T. J., and McLaughlin, J. B., 1991, ‘‘Large-Scale Com- vealed in 关15兴. The effect of Prandtl number 共Pr⫽1, 5, and 10兲 on puter Simulation of Fully Developed Turbulent Channel Flow With Heat the averaged heat flux, the temperature variance, the eddy diffu- Transfer,'' Int. J. Numer. Methods Fluids, 13, p. 999.
sivity, and the heat transfer scaling laws has been examined.
关7兴 Na, Y., Papavassiliou, D. V., and Hanratty, T. J., 1999, ‘‘Use of Direct Numeri- The changes in Pr were indeed found to affect the average cal Simulation to Study the Effect of Prandtl Number on Temperature Fields,''
Int. J. Heat Fluid Flow, 20, p. 187.
results, but in very much the same way as in available wall flow 关8兴 Campbell, J. A., and Hanratty, T. J., 1983, ‘‘Mechanisms of Turbulent Mass data. This was particularly true for the way the thickness of the Transfer at Solid Boundaries,'' AIChE J., 29, p. 221.
diffusive sublayer reduces with increasing Pr, and in reference to 关9兴 McCready, M. J., Vassiliadou, E., and Hanratty, T. J., 1986, ‘‘Computer Simu- the induced influence on the production of heat flux and variance.
lation of Turbulent Mass Transfer at a Mobile Interface,'' AIChE J., 32, p.
1108.
It was also noticed that the pressure diffusion and dissipation con- 关10兴 Calmet, I., and Magnaudet, J., 1997, ‘‘Large-Eddy Simulation of High- tributions to the normal heat flux balance change with varying Schmidt Number Mass Transfer in a Turbulent Channel Flow,'' Phys. Fluids, 9,
Prandtl number. The most relevant statistical quantities were found to scale with the friction velocity. This is an important 11兴 Piller, M., Nobile, E., and Hanratty, T. J., 2002, ‘‘DNS Study of Turbulent Transport at Low Prandtl Numbers in a Channel Flow,'' J. Fluid Mech., 458, p.
result, since the capillary waves are expected to modify the local rate of heat transfer only through a reduction of the frictional drag 关12兴 Lombardi, P., De Angelis, V., and Banerjee, S., 1996, ‘‘Direct Numerical in favor of form drag. This tendency accentuates with increasing Simulation of Near-Interface Turbulence in Coupled Gas-Liquid Flow,'' Phys.
waveslope caused by increasing u . In the present case, the im- Fluids, 8, p. 1643.
关13兴 De Angelis, V., Lombardi, P., and Banerjee, S., 1997, ‘‘Direct Numerical posed shear velocity at the beginning of the computations led to a Simulation of Turbulent Flow Over a Wavy Wall,'' Phys. Fluids, 9, p. 2429.
ratio of frictional drag to total drag 共including form drag兲 of 0.98.
关14兴 De Angelis, V., Lombardi, P., Andreussi, P., and Banerjee, S., 1997, ‘‘Micro- Physiscs of Scalar Transfer at Air-Water Interfaces,'' in Proceedings of Wind- Another important result is the appreciable effect of Pr on ␪⫹2, Over-Wave Couplings: Perspectives and Prospects, S. G. Sajjadi, N. H. Tho- and also on the thermal time scale ␶ mas, and J. C. R. Hunt, eds., Oxford University Press.
关15兴 Fulgosi, M., Lakehal, D., Banerjee, S., and De Angelis, V., 2003, ‘‘Direct cluded兲, indicating that the range of spectral functions for the Numerical Simulation of Turbulence in a Sheared Air-Water Flow With De- thermal fluctuating field increases with Pr.
formable Interface,'' J. Fluid Mech., 482, p. 319.
The scaling law for the normalized heat transfer velocity K⫹ on 关16兴 Delhaye, J. M., 1974, ‘‘Jump Conditions and Entropy Sources in Two-Phase Systems. Local Instant Formulation,'' Int. J. Multiphase Flow, 1, p. 305.
the gas side suggests an approximate Pr⫺3/5 relationship, varying 关17兴 Lakehal, D., Meier, M., and Fulgosi, M., 2002, ‘‘Interface Tracking Towards between Pr⫺1/2 for free surfaces and Pr⫺2/3 for immobile inter- the Direct Simulation of Heat and Mass Transfer in Multiphase Flows,'' Int. J.
faces and much higher Prandtl numbers. The parameterization of Heat Fluid Flow, 23, p. 242.
the heat transfer rates based on the surface renewal theory delivers 关18兴 Temam, R., 1979, Navier-Stokes Equations, North-Holland, Amsterdam.
关19兴 Tiselj, I., Bergant, R., Mavko, B., Bajsic, I., and Hetsroni, G., 2001, ‘‘DNS of values for the constant of proportionality and the Pr-power that Turbulent Heat Transfer in Channel Flow With Heat Conduction in the Solid conform with both the Leveque and the Polhausens boundary Wall,'' ASME J. Heat Transfer, 123, p. 849.
1138 Õ Vol. 125, DECEMBER 2003
Transactions of the ASME
关20兴 Phillips, O. M., 1997, The Dynamics of the Upper Ocean, Cambridge Univer- 关23兴 Banerjee, S., 1971, ‘‘A Note on Turbulent Mass Transfer at High Schmidt sity Press, Cambridge, UK.
Numbers,'' Chem. Eng. Sci., 26, p. 989.
关21兴 Tiselj, I., Pogrebnyak, E., Li, C., Mosyak, A., and Hetsroni, G., 2001, ‘‘Effect 关24兴 Lam, K., and Banerjee, S., 1992, ‘‘On the Condition of Streaks Formation in a of Wall Boundary Condition on Scalar Transfer in a Fully Developed Turbu- Bounded Turbulent Flow,'' Phys. Fluids A, 4, p. 306.
lent Flume,'' Phys. Fluids, 13共4兲, p. 1028.
关25兴 Nagano, Y., 2002, ‘‘Modelling Heat Transfer in Near-Wall Flows,'' in Closure 关22兴 Papavassiliou, D. V., and Hanratty, T. J., 1997, ‘‘Transport of a Passive Scalar Strategies for Turbulent and Transitional Flows, B. Launder and N. Sandham, in a Turbulent Channel Flow,'' Int. J. Heat Mass Transfer, 40, p. 1303.
eds., Cambridge University Press.
Journal of Heat Transfer
DECEMBER 2003, Vol. 125 Õ 1139

Source: http://ascomp.ch/download/Papers/JOURNALS/lakehal-fulgosi-jht1.pdf