Blacklight.fi

Duration of urination does not change with body sizePatricia J. Yanga, Jonathan Phama, Jerome Chooa, and David L. Hua,b,1 Schools of aMechanical Engineering and bBiology, Georgia Institute of Technology, Atlanta, GA 30332 Edited by David A. Weitz, Harvard University, Cambridge, MA, and approved May 14, 2014 (received for review February 6, 2014) Many urological studies rely on models of animals, such as rats and generate jets. Instead, they urinate using a series of drops, which pigs, but their relation to the human urinary system is poorly is shown by the 0.03-kg lesser dog-faced fruit bat and the 0.3-kg understood. Here, we elucidate the hydrodynamics of urination rat in Fig. 2 A–C, respectively.
across five orders of magnitude in body mass. Using high-speed Fig. 1H shows the urination time for 32 animals across six videography and flow-rate measurement obtained at Zoo Atlanta, orders of magnitude of body mass from 0.03 to 8,000 kg. De- we discover that all mammals above 3 kg in weight empty their spite this wide range in mass, urination time remains constant, bladders over nearly constant duration of 21 ± 13 s. This feat is T = 21 ± 13 s (n = 32), for all animals heavier than 3 kg. This possible, because larger animals have longer urethras and thus, invariance is noteworthy, considering that an elephant's blad- higher gravitational force and higher flow speed. Smaller mam- der, at 18 L, is nearly 3,600 times larger in volume than a cat's mals are challenged during urination by high viscous and capillary bladder at 5 mL. Using the method of least squares, we fit the forces that limit their urine to single drops. Our findings reveal data to a clear scaling law shown by the dashed line: T ∼ M0.13(Fig. 1H).
that the urethra is a flow-enhancing device, enabling the urinary For small animals, urination is a high-speed event of 0.01- to system to be scaled up by a factor of 3,600 in volume without 2-s duration and therefore, quite different from the behavior of compromising its function. This study may help to diagnose uri- the large animals observed that urinate for 21 s. Fig. 1H shows nary problems in animals as well as inspire the design of scalable urination time across 11 small animals, including one bat, five hydrodynamic systems based on those in nature.
rats, and five mice. Their body masses ranged from 0.03 to 0.3 kg.
The large error bar for the rats is caused by bladder fullness urology allometry scaling Bernoulli's principle varying across individuals. Fig. 2D shows the time course of theurine drop's radius measured by image analysis of high-speed Medical and veterinary urology often relies on simple, non- video of a rat. To rationalize the striking differences between invasive methods to characterize the health of the urinary large and small animals, we turn to mathematical modeling of system (1, 2). One of the most easily measured characteristics of the urinary system.
the urinary system is its flow rate (3), changes in which may beused to diagnose urinary problems. The expanding prostates of Modeling Assumptions. Urination may be simply described math- aging males may constrict the urethra, decreasing urine flow ematically. Fig. 1E shows a schematic of the urinary system, rate (4). Obesity may increase abdominal pressure, causing consisting of a bladder of volume V and the urethra, which is incontinence (5). Studies of these ailments and others often assumed to be a straight vertical pipe of length L and diameter involve animal subjects of a range of sizes (6). A study of D. We assume that the urethra has such a thin wall that its in-ternal and external diameters are equal. Urination begins when urination in zero gravity involved a rat suspended on two legs for the smooth muscles of the bladder pressurize the urine to P long periods of time (7), whereas other studies involve mice (8), measured relative to atmospheric pressure. After an initial tran- dogs (1), and pigs (9). Despite the wide range of animals used in sient of duration that depends on the system size, a steady flow of urological studies, the consequences of body size on urination speed u is generated.
remain poorly understood.
Previous medical and veterinary studies, particularly cystome- The bladder serves a number of functions, as reviewed by trography and ultrasonography, report substantial data on the Bentley (10). In desert animals, the bladder stores water to be anatomy, pressure, and flow rate of the urinary system. Fig. 3 retrieved at a time of need. In mammals, the bladder acts as shows urethral length (8, 15–25) and diameter (15, 24–34), flow a waterproof reservoir to be emptied at a time of convenience.
rate (35–42), bladder capacity (25, 43–49), and bladder pressure This control of urine enables animals to keep their homes sanitary (1, 35, 39, 40, 43, 46, 50) for over 100 individuals across 13 species.
and themselves inconspicuous to predators. Stored urine may evenbe used in defense, which one knows from handling rodents Several misconceptions in urology have important repercus- sions in the interpretation of healthy bladder function. For in- Animals eject fluids for waste elimination, communication, and stance, several investigators state that urinary flow is driven defense from predators. These diverse systems all rely on the entirely by bladder pressure. Consequently, their modeling of the fundamental principles of fluid mechanics, which we use to bladder neglects gravitational forces (11–13). Others, such as predict urination duration across a wide range of mammals. In Martin and Hillman (14), contend that urinary flow is driven by this study, we report a mathematical model that clarifies mis- a combination of both gravity and bladder pressure. In this study, conceptions in urology and unifies the results from 41 in- we elucidate the hydrodynamics of urination across animal size, dependent urological and anatomical studies. The theoretical showing the effects of gravity increase with increasing body size.
framework presented may be extended to study fluid ejectionfrom animals, a universal phenomenon that has received little In Vivo Experiments. We filmed the urination of 16 animals andobtained 28 videos of urination from YouTube, listed in Author contributions: P.J.Y. and D.L.H. designed research; J.P. and J.C. performed re- . show that urination style is strongly de- search; P.J.Y. and D.L.H. analyzed data; and P.J.Y. and D.L.H. wrote the paper.
pendent on animal size. Here, we define an animal as large if it is The authors declare no conflict of interest.
heavier than 3 kg and an animal as small if it is lighter than 1 kg.
This article is a PNAS Direct Submission.
Large animals, from dogs to elephants, produce jets and sheets 1To whom correspondence should be addressed. Email: of urine, which are shown in Fig. 1 A–D. Small animals, including This article contains supporting information online at rodents, bats, and juveniles of many mammalian species, cannot 11932–11937 PNAS August 19, 2014 vol. 111 no. 33

Jetting urination by large animals, including (A) elephant, (B) cow, (C) goat, and (D) dog. Inset of cow is reprinted from the public domain and cited in . (E) Schematic of the urinary system. (F) Ultrasound image of the bladder and urethra of a female human. The straight arrow indicates theurethra, and the curved arrow indicates the bladder. Reproduced with permission from ref. 20, (Copyright 2005, Radiological Society of North America). (G)Transverse histological sections of the urethra from a female pig. Reproduced with permission from ref. 9, (Copyright 2001, Elsevier). (H) The relationshipbetween body mass and urination time.
Table 1 shows the corresponding allometric relationships to be This shape factor is nearly constant across species and body used in numerical predictions for flow rate and urination time.
mass and consistent with the value of 0.17 found by Wheeler We begin by showing that the urinary system is isometric (i.e., et al. (55).
it has constant proportions across animal size). Fig. 3A shows Peak bladder pressure is difficult to measure in vivo, and in- the relation between body mass M and urethral dimensions stead, it is estimated using pressure transducers placed within the (length L and diameter D). As shown by the nearly parallel bladders of anesthetized animals. Pressure is measured when the trends for L and D (L = 35M0.43 and D = 2M0.39), the aspect bladder is filled to capacity by the injection of fluid. This tech- ratio of the urethra is 18. Moreover, the exponents are close to nique yields a nearly constant bladder pressure across animal the expected isometric scaling of M1/3. Fig. 3B shows the re- size: Pbladder = 5.2 ± 0.86 kPa (n = 8), which is shown in Fig. 3D.
lationship between body mass and bladder capacity. The bladder's The constancy of bladder pressure at 5.2 kPa is consistent with capacity is V ∼ M0.97, and the exponent of near unity indicates other systems in the body. One prominent example is the re- spiratory system, which generates pressures of 10 kPa for animals In ultrasonic imaging (Fig. 1F), the urethra appears circular spanning from a mosquito to an elephant (56).
(20). However, in histology (Fig. 1G), the urethra is clearlycorrugated, which decreases its cross-sectional area (9). The Steady-State Equation of Urine Flow. We model the flow as steady presence of such corrugation has been verified in studies in state and the urine as an incompressible fluid of density ρ, which flow is driven through the urethra (51, 52), although the viscosity μ, and surface tension σ. The energy equation re- precise shape has been too difficult to measure. We proceed lates the pressures involved, each of which has units of energy by using image analysis to measure cross-sectional area A per cross-sectional area of the urethra per unit length downthe urethra: from urethral histological diagrams of dead animals in theabsence of flow (9, 53, 54). We define a shape factor α = 4A/ πD2, which relates the urethral cross-sectional area with re- Pbladder + Pgravity = Pinertia + Pviscosity + Pcapillary: spect to that of a cylinder of diameter D. Fig. 3C shows theshape factor α = 0.2 ± 0.05 (n = 5) for which the corrected Each term in Eq. 1 may be written simply by considering the cross-sectional area is 20% of the original area considered.
pressure difference between the entrance and exit of the PNAS August 19, 2014 vol. 111 no. 33 11933

Dripping urination by small animals. (A) A rat's excreted urine drop. (B) A urine drop releasedby the lesser dog-faced fruit bat Cynopterus bra-chyotis. Courtesy of Kenny Breuer and SharonSwartz. (C) A rat's urine drop grows with time. Insetis reprinted from the public domain and cited in . (D) Time course of the drop radii of therat (triangles) along with prediction from our model(blue dotted line, α = 0.5; green solid line, α = 1; reddashed line, α = 0.2).
urethra. The combination of bladder and hydrostatic pressure our derivations here, however, we assume that the transient drives urine flow. Bladder pressure Pbladder is a constant given phase is negligible.
in Fig. 3D. We do not model the time-varying height in thebladder, because bladders vary greatly in shape (57). Thus, Large Animals Urinate for Constant Duration. Bladder pressure, hydrostatic pressure scales with urethral length: P gravity, and inertia are dominant for large animals, which can be gravity ∼ ρgL, where g is the acceleration of gravity. Dynamic pressure Pinertia shown by consideration of the dimensionless groups in scales as ρu2/2 and is associated with the inertia of the flow.
The viscous pressure drop in a long cylindrical pipe is given by the Darcy–Weisbach equation (58): Pviscosity = fD(Re)ρLu2/2αD.
αD as the effective diameter of the pipe to keep the cross- sectional area of the pipe consistent with experiments. TheDarcy friction factor f The urination time T, the time to completely empty the bladder, D is a function of the Reynolds number Re = ρuD/μ, such that f may be written as the ratio of bladder capacity to time-averaged D(Re) = 64/Re for laminar flow and flow rate, T = V/Q. We define the flow rate as Q = uA, where A = D(Re) = 0.316/Re1/4 for turbulent flow (104 < Re < 105). Drops generated from an orifice of effective diameter απD2/4 is the cross-sectional area of the urethra. Using Eq. 4 to a capillary force (59) of P substitute for flow speed yields αD. Substituting these terms into Eq. 1, we arrive at By isometry, bladder capacity V ∼ M and urethral length and The relative magnitudes of the five pressures enumerated in diameter both scale with M1/3; substitution of these scalings into Eq. 2 are prescribed by six dimensionless groups, including the Eq. 5 yields urination time T ∼ M1/6 ≈ M0.16 in the limit of in- aforementioned Reynolds number and Darcy friction factor creasing body mass. Agreement between predicted and mea- and well-known Froude Fr = u= gL and Bond Bo = ρgD2/σ sured scaling exponents is very good (0.13 compared with 0.16).
numbers (60) as well as dimensionless groups pertaining to the We, thus, conclude that our scaling has captured the observed urinary system, the urethra aspect ratio As = D/L, and pressure invariance in urination time.
ratio Pb = Pbladder/ρgL. Using these definitions, we nondimen- We go beyond a simple scaling by substituting the measured sionalize Eq. 2 to arrive at allometric relationships from Table 1 for L, D, α, V, and Pbladderinto Eq. 5, yielding a numerical prediction for urination time.
This prediction (Fig. 1H, solid line) is shown compared with ex- perimental values (Fig. 1H, dashed line). The general trend is captured quite well. We note that numerical values are under-predicted by a factor of three across animal masses, likely because In the following sections, we solve Eq. 3 in the limits of large and of the angle and cross-section of the urethra in vivo.
small animals.
How can an elephant empty its bladder as quickly as a cat? In we apply a variation of the Washburn law Larger animals have longer urethras and therefore, greater hy- (61) to show that the steady-state model given in Eq. 2 is drostatic pressure driving flow. Greater pressures lead to higher accurate for most animals. Animals lighter than 100 kg ach- flow rates, enabling the substantial bladders of larger animals to ieve 90% of their flow velocity within 4 s; however, for animals be emptied in the same duration as those of their much smaller such as elephants, the transient phase can be substantial. For

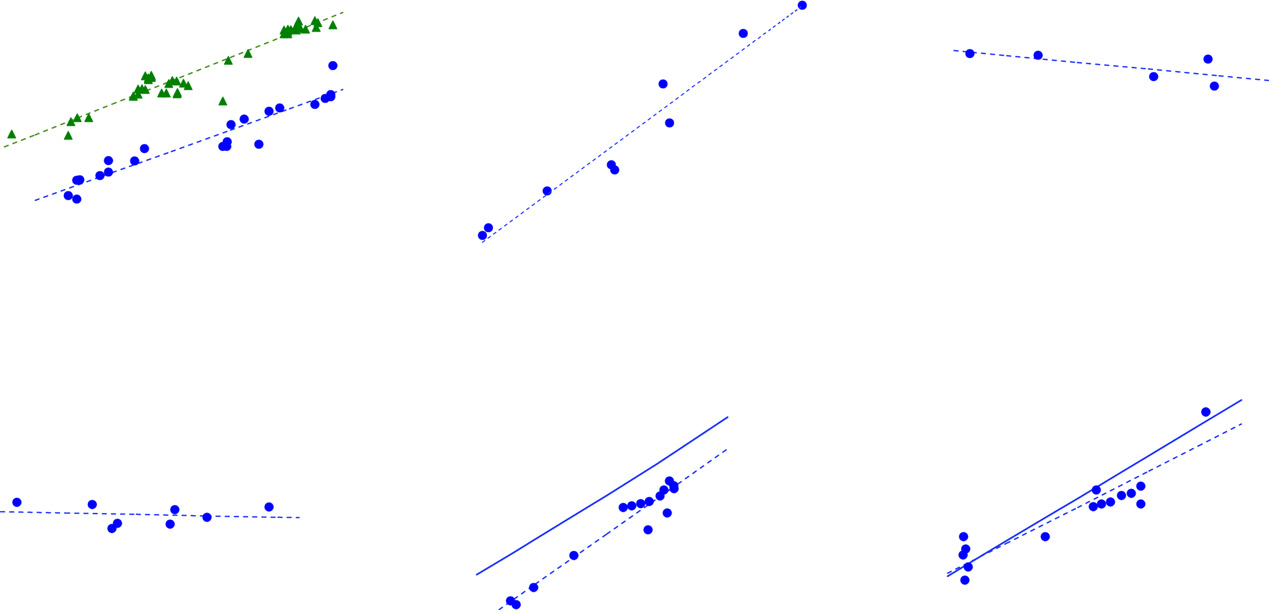
0.01 0.1 1 10 100 1000 0.01 0.1 1 10 100 1000 0.01 0.1 1 10 100 1000 0.01 0.1 1 10 100 1000 10000 0.1 1 10 100 The relation between body mass M and properties of the urinary system. (A) Urethral length L (green triangles) and diameter D (blue circles). (B) Bladder capacity V. (C) Shape factor α associated with the urethral cross-section. (D) Bladder pressure Pbladder. (E) Flow rate of males. (F) Flow rate of females.
Symbols represent experimental measurements, dashed lines represent best fits to the data, and solid lines represent predictions from our model.
Our model provides a consistent physical picture on consid- pressures and urethral anatomy (15, 16, 50) (Pbladder = 6.03 kPa, eration of flow rate. Combining Eq. 4 and the definition of flow L = 20 mm, D = 0.8 mm).
rate (Q = uA) yields To determine urination time, we turn to the dynamics of drop filling. A spherical drop is filled by the influx of urine, Q = απD2u/4.
By conservation of mass, dV drop/dt = Q, a first-order differential equation that may be easily integrated to obtain the drop volumeV(t). We assume that the initial drop corresponds to a sphere of the Our model gives insight into the distinct flow-rate scalings same diameter as the urethra, αD. Thus, the radius of the observed for both male and female mammals. Male mammals spherical urine drop may be written generally stand on four legs and have a penis that extends downward, enabling them to urinate vertically. Assuming isometry (D ∼ M1/3 and L ∼ M1/3), flow rate scales as Q ∼ M5/6 ≈ M0.83 in the limit of large body mass. This predicted exponent is with-in 10% of the observed scaling for males: QM ∼ M0.92. By sub-stituting the allometric relations from Table 1 into Eq. 6, we Combining Eq. 8 and the numerical solution for Eq. 7, we com- compute a numerical prediction for flow rate (Fig. 3E, solid line) pute the time course of the drop radius. This prediction is com- that is five times higher than experimental flow rates (Fig. 3E, pared with experimental values in Fig. 2D. We find that the dashed line). This overprediction is roughly consistent with our prediction is highly sensitive to the value of α. Without consid- underprediction for urination time.
eration of the corrugated cross-section, a prediction of α = 1 Female mammals have anatomy such that the urethral exit is (Fig. 2D, green solid line) yields a flow rate that is too high.
near the anus: thus, many female animals urinate horizontally.
Using the shape factor α = 0.2 (Fig. 2D, red dashed line), our The scaling of Eq. 6 without the gravitational term is Q ∼ M2/3 ≈ model predicts a flow speed of u = 1.2 m/s, which fits the data M0.67, and the exponent is in correspondence to that found in our fairly well. Using nonlinear least-squares fitting in Matlab, the experiments for females: Q best fit to the experimental data yields an intermediate value of F ∼ M0.66. Substituting allometric relations from Table 1 yields a numerical prediction (Fig. 3F, α = 0.5 (Fig. 2D, blue dotted line).
solid line) that remains in good agreement with experiments.
The drop does not grow without limit but falls when its gravi- tational force, scaling as 4πR3ρg=3, overcomes its attaching cap- Small Animals Urinate Quickly and for Constant Duration. Bladder illary force to the urethra, scaling as π αDσ. Equating these two pressure, viscous pressure, and capillary pressure are dominant forces yields the final drop radius before detachment, for small animals, which is shown by the associated dimension-less groups in In this limit, Eq. 2 reduces to which does a fair job of predicting the drop size. We predict drop which we solve numerically for flow speed u. To predict the flow radii for rats and mice of 1.3 and 1.1 mm, respectively, which are speed of a rat, inputs to this equation include the rat's bladder two times as large as experimental values of 2.0 ± 0.1 (n = 5) and PNAS August 19, 2014 vol. 111 no. 33 11935 Measured allometric relationships for the urinary urethra. In the medical literature, the function of the urethra was system of animals previously unknown. It was simply defined as a conduit betweenbladder and genitals. In this study, we find that the urethra is analogous to Pascal's Barrel: by providing a water-tight pipe to Duration of urination direct urine downward, the urethra increases the gravitational force acting on urine and therefore, the rate at which urine is Urethral diameter expelled from the body. Thus, the urethra is critical to the bladder's ability to empty quickly as the system is scaled up.
Engineers may apply this result to design a system of pipes and reservoirs for which the drainage time does not depend on system Flow rate for females size. This concept of a scalable hydrodynamic system may be used Flow rate for males in the design of portable reservoirs, such as water towers, waterbackpacks, and storage tanks.
Body mass M given in kilograms. Duration of urination corresponds to Why is urination time 21 s, and why is this time constant across animals heavier than 3 kg. Urethral length and diameter, shape factor, blad- animal sizes? The numerical value of 21 s arises from the un- der capacity, bladder pressure, and flow rates correspond to animals heavierthan 0.02 kg.
derlying physics involving the physical properties of urine as wellas the dimensions of the urinary system. Our model shows thatdifferences in bladder capacity are offset by differences in flow 2.2 ± 0.4 mm (n = 5), respectively. We suspect this difference is rate, resulting in a bladder emptying time that does not change caused by our underestimation of urethral perimeter at the exit.
with system size. Such invariance has been observed in a number For such a large drop to remain attached, we require the attach- of other systems. Examples include the height of a jump (64) and ment diameter to be larger by a factor of two, which is quite the number of heartbeats in a lifetime (65). Many of these examples possible, because the urethral exit is elliptical.
arise from some aspect of isometry, such as with our system.
Substituting Eq. 9 into Eq. 8, the time to eject one drop may From a biological perspective, the invariance of urination time suggests its low functional significance. Because bladder volume is 4.6 mL/kg body mass and daily urine voided is 26 mL/kg body mass (66), mammals urinate 5.6 times/d. Because the time to − 1 ≈ 4D cos θ urinate once is 21 s, the daily urination time is 2 min, which canbe translated to 0.2% of an animal's day, a negligible portion The predictions of maximum drop size and time to fall are in compared with other daily activities, such as eating and sleeping, excellent correspondence with observed values for rats and mice.
for which most animals take care to avoid predation. Thus, uri- Using Eq. 10, we predict drop falling times of 0.05 and 0.15 s for rats nation time likely does not influence animal fitness. The geometry and mice, respectively, which are nearly identical to experimental of the urethra, however, may play a role in other activities of values of 0.06 ± 0.05 (n = 5) and 0.14 ± 0.1 s (n = 14), respectively.
high functional significance, such as ejaculation.
A scaling for urine duration for small animals is not straight- In our study, we found that urination time is highly sensitive forward because of the nonlinearity of Eq. 7. We conduct a scaling to urethral cross-section. This dependency is particularly high for analysis in the limit of decreasing animal size for which the Rey- small animals for which urine flow is resisted by capillary and nolds number approaches zero. Because of isometry, V ∼ M and D ∼ viscous forces, which scale with the perimeter of the urethra. More M1/3. Rewriting Eq. 7 at low Reynolds number, we have u ∼ D, accurate predictions for small animals require measurements of and therefore, the time to eject one drop from Eq. 10 scales as the urethral exit perimeter and the urethral cross-section, which is Tdrop ∼ Bo−1 ∼ M−2/3. Using Eq. 9, the final drop size is Rf ∼ D ∼ M1/3.
known to vary with distance down the urethra (67). Current By conservation of mass, a full bladder of volume V can produce models of noncircular pipe flow are not applicable, because they N spherical drops, where N = 3V =4πR3 ∼ M2=3. Thus, the urina- only account for infinitesimal corrugations (68). Additional math- tion time for small animals T = NTdrop is constant and there- ematical techniques as well as accurate urethral measurements fore, independent of animal size. This prediction indicates are needed to increase correspondence with experiments.
that small animals urinate for different durations than largeanimals, which is in correspondence with experiments. Our Materials and Methods experiments indicate that mammals of mass 0.03–0.3 kg uri- We filmed urination of animals using both Sony HDR-XR200 and high-speed nate for durations of 0.1–2 s. We have insufficient range of cameras (Vision Research v210 and Miro 4). The masses of animals are taken masses for small animals to conclude our prediction that from annual veterinary procedures or measured using an analytical balance.
urination time is constant in this regime.
Flow rate Q is measured by simultaneous high-speed videography and The model yields insight into the challenges faced by small manual urine collection using containers of appropriate size and shape. We animals. In Eq. 7, flow speed is positive only if Pbladder αD ≥ 4σ, use the open-source software Tracker to measure the time course of the where σ is the surface tension of urine, which for humans is com- radius of urine drops produced by rats and mice.
parable with the surface tension of water (62). Thus, we predictthat the smallest urethra to expel urine has a diameter of ACKNOWLEDGMENTS. We acknowledge photographer C. Hobbs and our 4σ= αPbladder ∼ 0:1  mm. According to our allometric trends, the hosts at Zoo Atlanta (R. Snyder), the University of Georgia (L. Elly), the smallest animal that can urinate independently corresponds to Atlanta Humane Society (A. Lopez), and the animal facilities at Georgia Tech a body mass of 0.8 g and urethral length of 1.7 mm. This mass (L. O'Farrell). We thank YouTube contributors, including Alex Cobb, Cole corresponds to that of altricial mice (0.5–3 g), which are de- Onyx, demondragon115, drakar2835, ElMachoPrieto83, Ilze Darguze, Joe pendent on their mother's licking of excreted urine drops (63).
BERGMANN, Joey Ponticello, krazyboy35, laupuihang, MegaTobi89, Mixetc,mpwhat, MrTitanReign, relacsed, RGarrido121, ronshausen63, Sandro Puelles, Silvia Lugli, and Tom Holloway. Our funding sources were National ScienceFoundation Faculty Early Career Development Program (Division of Physics) The urinary system works effectively across a range of length scales.
Grant 1255127 for the modeling and Georgia Tech President's Undergraduate This robustness is caused by the hydrodynamic contribution of the Research Awards for the experiments.
1. Hinman F (1971) Hydrodynamics of Micturition (Thomas, New York).
3. Schäfer W, et al.; International Continence Society (2002) Good urodynamic practices: 2. Griffiths DJ (1973) The mechanics of the urethra and of micturition. Br J Urol 45(5): Uroflowmetry, filling cystometry, and pressure-flow studies. Neurourol Urodyn 21(3): 4. Girman CJ, et al. (1995) Natural history of prostatism: Relationship among symptoms, 36. Gutierrez Segura C (1997) Urine flow in childhood: A study of flow chart parameters prostate volume and peak urinary flow rate. J Urol 153(5):1510–1515.
based on 1,361 uroflowmetry tests. J Urol 157(4):1426–1428.
5. Dwyer PL, Lee ET, Hay DM (1988) Obesity and urinary incontinence in women. Br J 37. Madersbacher S, et al. (1998) The aging lower urinary tract: A comparative urody- Obstet Gynaecol 95(1):91–96.
namic study of men and women. Urology 51(2):206–212.
6. Sibley GN (1984) A comparison of spontaneous and nerve-mediated activity in blad- 38. Nitti VW, Tu LM, Gitlin J (1999) Diagnosing bladder outlet obstruction in women.
der muscle from man, pig and rabbit. J Physiol 354:431–443.
J Urol 161(5):1535–1540.
7. Ortiz RM, Wang TJ, Wade CE (1999) Influence of centrifugation and hindlimb sus- 39. Van Asselt E, Groen J, Van Mastrigt R (1995) A comparative study of voiding in rat and pension on testosterone and corticosterone excretion in rats. Aviat Space Environ guinea pig: Simultaneous measurement of flow rate and pressure. Am J Physiol 269(1 Pt 2):R98–R103.
8. St Clair MB, Sowers AL, Davis JA, Rhodes LL (1999) Urinary bladder catheterization of 40. Schmidt F, Yoshimura Y, Shin PY, Constantinou CE (2003) Comparative urodynamic female mice and rats. Contemp Top Lab Anim Sci 38(3):78–79.
patterns of bladder pressure, contractility and urine flow in man and rat during 9. Dass N, McMurray G, Greenland JE, Brading AF (2001) Morphological aspects of the micturition. APMIS Suppl 109(2003):39–44.
female pig bladder neck and urethra: Quantitative analysis using computer assisted 3- 41. Masumori N, et al. (1996) Japanese men have smaller prostate volumes but compa- dimensional reconstructions. J Urol 165(4):1294–1299.
rable urinary flow rates relative to American men: Results of community based studies 10. Bentley PJ (1979) The vertebrate urinary bladder: Osmoregulatory and other uses.
in 2 countries. J Urol 155(4):1324–1327.
Yale J Biol Med 52(6):563–568.
42. Folkestad B, Spångberg A (2004) Timed micturition and maximum urinary flow rate in 11. Rao SG, Walter JS, Jamnia A, Wheeler JS, Damaser MS (2003) Predicting urethral area from randomly selected symptom-free males. Scand J Urol Nephrol 38(2):136–142.
video-urodynamics in women with voiding dysfunction. Neurourol Urodyn 22(4):277–283.
43. Pandita RK, Fujiwara M, Alm P, Andersson K-E (2000) Cystometric evaluation of 12. Walter JS, Wheeler JS, Morgan C, Plishka M (1993) Urodynamic evaluation of urethral bladder function in non-anesthetized mice with and without bladder outlet ob- opening area in females with stress incontinence. Int Urogynecol J 4(6):335–341.
struction. J Urol 164(4):1385–1389.
13. Barnea O, Gillon G (2001) Model-based estimation of male urethral resistance and 44. Birder LA, et al. (2002) Altered urinary bladder function in mice lacking the vanilloid elasticity using pressure-flow data. Comput Biol Med 31(1):27–40.
receptor TRPV1. Nat Neurosci 5(9):856–860.
14. Martin JA, Hillman SS (2009) The physical movement of urine from the kidneys to the 45. Herrera GM, Meredith AL (2010) Diurnal variation in urodynamics of rat. PLoS ONE urinary bladder and bladder compliance in two anurans. Physiol Biochem Zool 82(2): 46. Thor KB, Katofiasc MA (1995) Effects of duloxetine, a combined serotonin and norepi- 15. Chang S, Chern I, Bown SG (2000) Photodynamic therapy of rat bladder and urethra: nephrine reuptake inhibitor, on central neural control of lower urinary tract function in Evaluation of urinary and reproductive function after inducing protoporphyrin IX the chloralose-anesthetized female cat. J Pharmacol Exp Ther 274(2):1014–1024.
with 5-aminolaevulinic acid. BJU Int 85(6):747–753.
47. Abdel-Gawad M, Boyer S, Sawan M, Elhilali MM (2001) Reduction of bladder outlet 16. Kamo I, et al. (2004) The role of bladder-to-urethral reflexes in urinary continence resistance by selective stimulation of the ventral sacral root using high frequency mechanisms in rats. Am J Physiol Renal Physiol 287(3):F434–F441.
blockade: A chronic study in spinal cord transected dogs. J Urol 166(2):728–733.
17. Vogel H (2007) Drug Discovery and Evaluation: Pharmacological Assays (Springer, 48. Atalan G, Barr FJ, Holt PE (1998) Estimation of bladder volume using ultrasonographic New York), 3rd Ed.
determination of cross-sectional areas and linear measurements. Vet Radiol Ultra- 18. Johnston GR, Osborne CA, Jessen CR (1985) Effects of urinary bladder distension on the length of the dog and cat urethra. Am J Vet Res 46(2):509–512.
49. Higgins AJ, Snyder JR (2006) The Equine Manual (Elsevier Saunders, Philadelphia).
19. Takeda M, Lepor H (1995) Nitric oxide synthase in dog urethra: A histochemical and 50. Ishizuka O, et al. (1996) Micturition in conscious rats with and without bladder pharmacological analysis. Br J Pharmacol 116(5):2517–2523.
outlet obstruction: Role of spinal α 1-adrenoceptors. Br J Pharmacol 117(5): 20. Prasad SR, et al. (2005) Cross-sectional imaging of the female urethra: Technique and results. Radiographics 25(3):749–761.
51. Pullan BR, Phillips JI, Hickey DS (1982) Urethral lumen cross-sectional shape: Its ra- 21. Kohler TS, Yadven M, Manvar A, Liu N, Monga M (2008) The length of the male diological determination and relationship to function. Br J Urol 54(4):399–407.
urethra. Int Braz J Urol 34(4):451–454, discussion 455–456.
52. Fonda D, Hickey DS, Brocklehurst JC (1985) Dynamic shape of the female urethra 22. Lueders I, Luther I, Scheepers G, van der Horst G (2012) Improved semen collection during micturition. Clinical methods. J Urol 134(1):88–91.
method for wild felids: Urethral catheterization yields high sperm quality in African 53. Treuting P, Dintzis SM (2011) Comparative Anatomy and Histology: A Mouse and lions (Panthera leo). Theriogenology 78(3):696–701.
Human Atlas (Academic, Waltham, MA).
23. Balke JM, Boever WJ, Ellersieck MR, Seal US, Smith DA (1988) Anatomy of the 54. Praud C, Sebe P, Mondet F, Sebille A (2003) The striated urethral sphincter in female reproductive tract of the female African elephant (Loxodonta africana) with rats. Anat Embryol (Berl) 207(2):169–175.
reference to development of techniques for artificial breeding. J Reprod Fertil 55. Wheeler AP, Morad S, Buchholz N, Knight MM (2012) The shape of the urine stream— from biophysics to diagnostics. PLoS ONE 7(10):e47133.
24. Hildebrandt TB, et al. (2000) Ultrasonography of the urogenital tract in elephants 56. Kim W, Bush JWM (2012) Natural drinking strategies. J Fluid Mech 705:7–25.
(Loxodonta africana and Elephas maximus): An important tool for assessing female 57. Damaser MS, Lehman SL (1995) The effect of urinary bladder shape on its mechanics reproductive function. Zoo Biol 19(5):321–332.
during filling. J Biomech 28(6):725–732.
25. Fowler ME, Mikota SK (2006) Biology, Medicine, and Surgery of Elephants (Wiley- 58. Ghiaasiaan S (2011) Convective Heat and Mass Transfer (Cambridge Univ Press, Blackwell, Hoboken, NJ).
Cambridge, United Kingdom).
26. Souza AB, et al. (2008) Comparison of two experimental models of urodynamic 59. de Gennes P-G, Brochard-Wyart F, Quéré D (2004) Capillarity and Wetting Phenom- evaluation in female rats. Acta Cir Bras 23(Suppl 1):59–65.
ena: Drops, Bubbles, Pearls, Waves (Springer, New York).
27. Russell B, Baumann M, Heidkamp MC, Svanborg A (1996) Morphometry of the aging 60. Vogel S (1994) Life in Moving Fluids: The Physical Biology of Flow (Princeton Univ female rat urethra. Int Urogynecol J Pelvic Floor Dysfunct 7(1):30–36.
Press, Princeton).
28. Kunstỳr I, Küpper W, Weisser H, Naumann S, Messow C (1982) Urethral plug-a new 61. Bush JWM (2010) 18.357 Interfacial Phenomena, Fall 2010. Available at secondary male sex characteristic in rat and other rodents. Lab Anim 16(2):151–155.
Accessed May 2, 2014.
29. Root MV, Johnston SD, Johnston GR, Olson PN (1996) The effect of prepuberal and 62. Ogata M, Tomokuni K, Takatsuka Y (1970) Urinary excretion of hippuric acid and m- postpuberal gonadectomy on penile extrusion and urethral diameter in the domestic or p-methylhippuric acid in the urine of persons exposed to vapours of toluene and cat. Vet Radiol Ultrasound 37(5):363–366.
m- or p-xylene as a test of exposure. Br J Ind Med 27(1):43–50.
30. Gray H (1918) Anatomy of the Human Body (Lea and Febiger, Philadelphia).
63. Moore CL, Chadwick-Dias A-M (1986) Behavioral responses of infant rats to maternal 31. Tsujimoto Y, Nose Y, Ohba K (2003) Experimental and clinical trial of measuring licking: Variations with age and sex. Dev Psychobiol 19(5):427–438.
urinary velocity with the pitot tube and a transrectal ultrasound guided video ur- 64. McMahon TA, Bonner JT, Freeman W (1983) On Size and Life (Freeman, New York).
odynamic system. Int J Urol 10(1):30–35.
65. Schmidt-Nielsen K (1984) Scaling: Why Is Animal Size So Important? (Cambridge Univ 32. Pozor MA, McDonnell SM (2002) Ultrasonographic measurements of accessory sex Press, Cambridge, United Kingdom).
glands, ampullae, and urethra of normal stallions of various size types. Theriogenology 66. Dukes H, Reece W (2004) Dukes' Physiology of Domestic Animals, G - Reference, In- formation and Interdisciplinary Subjects Series (Comstock Publishing Associates, 33. Bailey C (1975) Siliceous urinary calculi in bulls, steers, and partial castrates. Can J Ithaca, NY), 12th Ed.
Anim Sci 55(2):187–191.
67. Woodburne RT, Lapides J (1972) The ureteral lumen during peristalsis. Am J Anat 34. Hildebrandt TB, et al. (1998) Reproductive assessment of male elephants (Loxodonta africana and Elephas maximus) by ultrasonography. J Zoo Wildl Med 29(2):114–128.
68. Mortensen NA, Okkels F, Bruus H (2005) Reexamination of Hagen-Poiseuille flow: 35. Walter JS, et al. (2005) Bladder-wall and pelvic-plexus stimulation with model mi- Shape dependence of the hydraulic resistance in microchannels. Phys Rev E Stat crostimulators: Preliminary observations. J Rehabil Res Dev 42(2):251–260.
Nonlin Soft Matter Phys 71(5 Pt 2):057301.
PNAS August 19, 2014 vol. 111 no. 33 11937 Supporting Videos Video S1. Urination of a rat, mass of 0.24 kg. Time slowed by 33 X.
Video S2. Urination of a goat, mass of 70 kg. Time slowed by 17 X.
Video S3. Urination of a cow, mass of 640 kg. Time slowed by 33 X.
Video S4. Urination of an elephant, mass of 3540 kg. Time slowed by 33 X.
Unsteady hydrodynamic urination model for large and small animals In this section, we estimate the time for the urine flow to achieve steady state. The column of urinedescends due to gravitational and bladder pressure forces. This descent is resisted by viscosity,fluid inertia and capillary pressure.
At time t = 0 the urethra is empty. We parametrize the height of urine in the urethra with a height z(t), measured from the bladder. Consider Figure 1E in the main text. We consider a con-trol volume including the mass of urine with the bladder and urethra. Conservation of momentumfor this control volume may be written z = A (Pbladder + Pgravity − Pinertia − Pviscosity − Pcapillary) .
Each terms in Equation (1) has units of force and may be written simply. The mass of urine in theurethra is m = ρπαD2z/4. Using techniques presented by Bush∗, the added mass associated withacceleration of fluid in the bladder may be written ma = 7ρπα3/2D3/48 . Bladder pressure Pbladderis constant. Hydrostatic pressure Pgravity scales as ρgz where g is the gravitational acceleration.
Dynamic pressure Pinertia scales as ρ ˙z2/2, and is associated with inertia of the flow. Assuminglaminar flow, the pressure drop due to viscosity in a long cylindrical pipe is Pviscosity = 32µz ˙z/αD2.
The capillary force of drops generated from an orifice of effective diameter αD is Pcapillary = 4σ/ αD. Substituting these terms into Equation (1), we arrive at We compute velocity ˙ z in Equation (2) using a Runge-Kutta single-step solver (ode45) in Matlab.
Inputs to this equation include allometric relationships of bladder pressure, urethral diameter, andshape factor, given in Table 1. Figure S1 shows the time course of urine velocity. For animallighter than 100 kg, the flow reaches 90% of its final velocity in 4 seconds, which is 15% of the thetime to empty the bladder, 21 seconds. We thus conclude our steady state model reported in themain text is accurate for animals lighter than 100 kg. For larger animals such as elephants, thetransition can be substantial.
∗Bush JWM (2010) 18.357 Interfacial Phenomena, Fall 2010. Avaliable at http://ocw.mit.edu Accessed 2 May, Figure S1. Time course of urine velocity.
less G 100
Mass (kg)
Figure S2. Values of dimensionless groups including the Froude Fr, Bond Bo, Reynolds Re, aspect ratioAs, and ratio of bladder and hydrostatic pressure Pb.
Table S1. Duration of urination. Mass (kg)
Duration (s)
Experiment at Georgia Tech K. Breuer and S. Swartz, Brown University Experiment at Georgia Tech Applehead Chihuahua Experiment at local park Youtube, Mattern (2000) Experiment at Zoo Atlanta Experiment at Zoo Atlanta Youtube, Wilcox (1997) Youtube, Wilcox (1997) Youtube, Wilcox (1997) Youtube, Wilson (2001) Youtube, Mil er (1997) Youtube, Brown (1996) Youtube, Starkey (1992) Youtube, Nowak (1999) Youtube, Lynette (2013) Youtube, Lynette (2013) Youtube, Linnaeus (1758) Youtube, Kingdon (1988) Youtube, Marvin (1992) Youtube, Marvin (1992) Youtube, Marvin (1992) Youtube, Bongianni (1988) Youtube, Potts (1997) Indian Rhinoceros Youtube, Toon (2002) Youtube, Toon (2002) Youtube, Toon (2002) Youtube, Toon (2002) Experiment at Zoo Atlanta Youtube, Shoshani (1982) Youtube, Shoshani (1982) Youtube, Shoshani (1982) Youtube, Shoshani (1982) Youtube, Shoshani (1982) Youtube, Shoshani (1982) Table S2. Urethral length. Mass (kg)
Length (mm)
Wister Rat (N=20) Sprague-Dawley Rat (N=61) Dunkin Hartley Guinea Pig Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Cat Normal Adult Dog Normal Adult Dog Normal Adult Dog Normal Adult Dog Normal Adult Dog Mongrel Dog (N=10) Normal Adult Dog Normal Adult Dog Normal Adult Dog Prasad (2005), Ogden (2004) African Lion (N=7) Lueders (2012), Nowak (1999) African Elephant (5 years) Balke (1988), Krumrey (1968) African Elephant (5 years) Balke (1988), Krumrey (1968) African Elephant (6 years) Balke (1988), Krumrey (1968) African Elephant (6 years) Balke (1988), Krumrey (1968) African Elephant (6 years) Balke (1988), Krumrey (1968) African Elephant (7 years) Balke (1988), Krumrey (1968) African Elephant (9 years) Balke (1988), Krumrey (1968) African Elephant (9 years) Balke (1988), Krumrey (1968) African Elephant (9 years) Balke (1988), Krumrey (1968) African Elephant (10 years) Balke (1988), Krumrey (1968) African Elephant (10 years) Balke (1988), Krumrey (1968) African Elephant (10 years) Balke (1988), Krumrey (1968) African Elephant (11 years) Balke (1988), Krumrey (1968) African Elephant (14 years) Balke (1988), Krumrey (1968) Hildebrandt (2000), Nowak (1999) African Elephant (23 years) Balke (1988), Krumrey (1968) African Elephant (25 years) Balke (1988), Krumrey (1968) Fowler (2006), Nowak (1999) Table S3. Urethral diameter. Mass (kg)
Diameter (mm)
Wister Rat (N=10) Hybrid Rat (12 months) (N=5) Russel (1996), Tasaki (2009) Hybrid Rat (32 months) (N=5) Russel (1996), Tasaki (2009) Adult Rat (N=176) Kunstyvr (1982), Perrin (2003) Short Hair Cat (7 weeks) (N=6) Root (1996), Sturman (1985) Short Hair Cat (7 weeks) (N=6) Root (1996), Sturman (1985) Short Hair Cat (7 months) (N=5) Root (1996), Scott (1970) Short Hair Cat (7 months) (N=5) Root (1996), Lein (1983) Gray (1918), Ogden (2004) Gray (1918), Ogden (2004) Man (71.7 years) (N=32) Tsujimoto (2003), Ogden (2004) Miniature Horse (N=7) Hereford X Angus Bul (N=96) Light Horse (N=53) Heavy Horse (N=15) Hildebrandt (2000), Nowak (1999) African Elephant (N=6) Hildebrandt (1998) Asian Elephant (N=2) Hildebrandt (1998) Hildebrandt (1998) Table S4. Shape factor, bladder capacity, and bladder pressure. Mass (kg)
Shape factor α
Caceci, Johnston (1985) Skarva, Ogden (2004) Mass (kg)
Bladder capacity (mL)
Sprague Dawley Rat Applehead Chihuahua Experiment at local park Mongrel Dog (N=14) Fowler (2006), Shoshani (1982) Mass (kg)
Bladder pressure (kPa)
Sprague Dawley Rat (N=7) Wister Rat (N=3) Sprague Dawley Rat (N=18) Table S5. Urine flow rate. Mass (kg)
Flow rate (mL/s)
Experiment at Georgia Tech Experiment at Georgia Tech Experiment at Georgia Tech Experiment at Georgia Tech Experiment at Georgia Tech Woman (3-4 years) Segura (1997), Ogden (2004) Woman (5-6 years) Segura (1997), Ogden (2004) Woman (7-8 years) Segura (1997), Ogden (2004) Woman (9-11 years) Segura (1997), Ogden (2004) Woman (12-14 years) Segura (1997), Ogden (2004) Experiment at local park Woman (59 years) (N = 183) Madersbacher (1998) , Ogden (2004) Woman (55 years) (N = 185) Nitti (1999) , Ogden (2004) L. Ely, University of Georgia L. Ely, University of Georgia Wister Rat (N=2) Sprague Dawley Rat (N=18) Dunkin Hartley Guinea Pig (N=4) Applehead Chihuahua Experiment at local park Segura (1997), Ogden (2004) Segura (1997), Ogden (2004) Segura (1997), Ogden (2004) Man (9-11 years) Segura (1997), Ogden (2004) Man (12-14 years) Segura (1997), Ogden (2004) Nigerian Dwarf Goat Experiment at Zoo Atlanta Experiment at Zoo Atlanta Japanese Man (N=271) Schmidt (2003), Schmidt (2002) American Man (N=467) Man (53.8 years) (N=58) Folkestad (2004), Ogden (2004) Table S6. Bibliography for images and animal masses. Online Image
Man vyi. (2005) Jersey cattle in Jersey, Wikimedia Commons Inset in Figure 1(c) http://commons.wikimedia.org/wiki/File:Jersey_cattle_in_Jersey.jpg
Stephens, J. (1992) Lobund-Wistar Rat Inset in Figure 2(b) https://visualsonline.cancer.gov/details.cfm?imageid=2568
Animal silhouettes Public Domain Pictures in Figure 1(h)
http://www.publicdomainpictures.net/ Caceci, T. (2008) Canine penis; H&E stain, paraffin section (decalcified), 20x, VM8054: Veterinary Histology Skarva, F. Cross-Section of a Normal Human Penis Showing the Urethra and Corpora Spongiosum, H&E Stain, LM X12 Body masses of animals considered
Nowak RM, Paradiso JL (1999) Walker's mammals of the world (The Johns Hopkins University Press, Baltimore, MD) Vol. 1, 6th Ed. Mattern MY, McLennan DA (2000) Phylogeny and speciation of felids. Cladistics 16(2):232–253. Wilcox C (1997) The Great Dane (Capstone, North Mankato, MN). Wilson D, Burnie D (2001) Animal: the definitive visual guide to the world's wildlife (DK Publishing, New York). Mil er-Schroeder P (1997) Goril as (Raintree Steck-Vaughn, Austin, TX). Brown G (1996) The Great Bear Almanac (Globe Pequot, Guilford, CT). Starkey P, Mwenya E, Stares J (1994) Improving animal traction technology. Proceedings of the First Workshop of the Animal Traction Network for Eastern and Southern Africa held 18-23 January 1992, Lusaka, Zambia (Technical Centre for Agricultural and Rural Cooperation, Wageningen, The Netherlands). Lynette R (2013) South American Tapirs (Bearport Publishing, New York). Linnaeus C (1758) Systema naturae per regna tria naturae, secundum classes, ordines, genera, species, cum characteribus, differenti s, synonymis, locis. (Laurenti Salvii, Stockholm), 10th Ed. Kingdon J (1988) East African Mammals: An Atlas of Evolution in Africa, Part A: Carnivores (University of Chicago Press, Chicago) Vol. 3. Hal MH, Comerford PM (1992) Pasture and hay for horses. Cooperative Extension, The Pennsylvania State University 32:1–4. Bongianni M (1988) Simon and Schuster's guide to horses and ponies of the world (Simon and Schuster, New York). Potts S (1997) The American Bison (Capstone, Mankato, MN). Toon A, Toon S (2002) Rhinos (Voyageur Press, Minneapolis, MN). Shoshani J, Eisenberg JF (1982) Elephas maximus. Mammalian Species 182:1–8. Ogden CL, Fryar CD, Carrol MD, Flegal KM (2004) Mean Body Weight, Height, and Body Mass Index: United States 1960-2002 (Department of Health and Human Services, Centers for Disease Control and Prevention, National Center for Health Statistics). Krumrey WA, Buss IO (1968) Age estimation, growth, and relationships between body dimensions of the female African elephant. Journal of Mammalogy 49(1):22–31. Tasaki M, et al. (2009) Simultaneous induction of non-neoplastic and neoplastic lesions with highly proliferative hepatocytes fol owing dietary exposure of rats to tocotrienol for 2 years. Archives of Toxicology 83(11):1021–1030. Perrin D, Soulage C, Pequignot J, Geloen A (2003) Resistance to obesity in Lou/C rats prevents ageing-associated metabolic alterations. Diabetologia 46(11):1489–1496. Sturman J, Moretz R, French J, Wisniewski H (1985) Postnatal taurine deficiency in the kitten results in a persistence of the cerebel ar external granule cel layer: correction by taurine feeding. Journal of Neuroscience Research 13(4):521–528. Scott P, Hafez E (1970) Reproduction and Breeding Techniques for Laboratory Animals. (Lea and Febiger, Philadelphia). Lein D, Concannon P (1983) Infertility and fertility treatments and management in the queen and tomcat. Current Therapy VIII. Kirk, R.(ed). (Elsevier Saunders, Philadelphia) 936–987. Schmidt F, Shin P, Jorgensen TM, Djurhuus JC, Constantinou CE (2002) Urodynamic patterns of normal male micturition: Influence of water consumption on urine production and detrusor function. The Journal of Urology 168(4 Pt 1):1458–1463. Supporting Information Yang et al. 10.1073/pnas.1402289111 Urination of a rat (mass of 0.24 kg). Time slowed by 33 times.
Urination of a goat (mass of 70 kg). Time slowed by 17 times.
Urination of a cow (mass of 640 kg). Time slowed by 33 times.
Urination of an elephant (mass of 3,540 kg). Time slowed by 33 times.
Other Supporting Information Files

Source: http://blacklight.fi/~jok/yang.pdf