Kamagra gibt es auch als Kautabletten, die sich schneller auflösen als normale Pillen. Manche Patienten empfinden das als angenehmer. Wer sich informieren will, findet Hinweise unter kamagra kautabletten.
Gji1599.tex
Geophysical Journal International
Geophys. J. Int. (2002)
148, 256–277
Morphological dating of cumulative reverse fault scarps: examples
from the Gurvan Bogd fault system, Mongolia
S. Carretier,1,∗ J-F Ritz,1 J. Jackson2 and A. Bayasgalan21
Laboratoire de G´eophysique Tectonique et S´edimentologie, CNRS-UMR, Universit´e Montpellier II, 4, Place Eug ene Bataillon, 34000 Montpellier, France.
E-mail: [email protected]2
Bullard Laboratories, Madingley Road, Cambridge, CB3 OEZ England
Accepted 2001 September 20. Received 2001 July 3; in original form 2000 August 10
S U M M A R Y
We relate reverse fault scarp morphology formed by several earthquake dislocations to the
average deformation rate, using a morphological dating model based on a diffusion analogue of
erosion. Our scarp degradation model includes diffusive erosion during the interseismic period,
the gravitational collapse of the coseismic fault scarp just after formation, and the variation of
the surface rupture location. Interactions between thrusting and geomorphic processes acting
on scarp morphology are analysed along the Gurvan Bogd Range in Mongolia. Four main
processes acting on scarp morphology were distinguished: 1) gravitational collapse of the
frontal scarp, resetting the diffusive scarp if fault offsets are big and faulting is localized; 2)
progressive erosion of the fault scarp during the interseismic period; 3) folding associated with
the frontal thrust and backthrusts; 4) competing alluvial deposition on mountain piedmont
slopes and abrasion of the fault scarp by wash processes. The growth of cumulative reverse
fault scarps is suppressed when they are located in the outwash of major drainage basins. They
can grow higher in distance from major catchment discharges. The modelling suggests that
the morphology of the scarp and its apparent degradation stage, depend on the parameters
controlling the amount of frontal collapse; the magnitude of coseismic offsets, the dip of the
fault near the surface and the step distance between faults. Folding associated with thrusting
creates a convexity on the upper part of the scarp and increases its height. The comparison
of different scarp profiles suggests that folding leads to an overestimate of the morphological
age. We estimate a diffusion coefficient at 3
.3 ± 1
.7 m2 ka−1. Morphological ages calculated
with our model confirm that slip rate along reverse faults of the Gurvan Bogd range has not
been constant over the last 100 ka.
Key words: cumulative fault scarp, earthquake, erosion, morphological dating, reverse
faulting, uplift rate.
marker according to the rates of vertical movement and erosion.
Morphological dating has been applied mainly in the cases of one-
Dating geomorphic features is one of the main problems in quan-
event fault scarps, terrace risers (e.g. Nash 1984; Hanks & Schwartz
titative geomorphology, especially applied to active tectonics. In
1987; Enzel
et al. 1996) and cumulative normal fault scarps (Avouac
addition to the recent development of numerical dating methods
& Peltzer 1993; Nash 1981). In this paper, we are concerned
(e.g. surface exposure dating using cosmonucleides—e.g. Brown
with estimating slip rates from morphological dating of cumula-
et al. 1991; Bierman
et al. 1995; Ritz
et al. 1995; Siame
et al.
tive reverse fault scarps found in the Gurvan Bogd fault system in
1997; Bourl es 1992), numerical modelling of landscape evolution
has opened the way to what is called morphological dating (e.g.
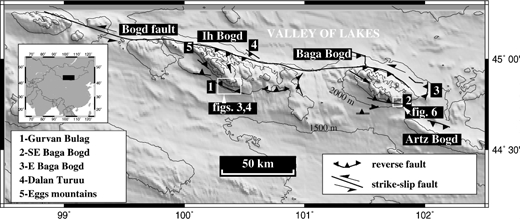
The Gurvan Bogd range forms the eastern terminus of the Gobi
Culling 1960; Hirano 1968; Bucknam & Anderson 1978; Nash
Altay mountain range of Mongolia (Fig. 1), and is composed of
1984; Hanks 1999). This approach is useful in studies of active
three massifs (Ih Bogd, Baga Bogd, Artz Bogd) corresponding to
tectonics because it allows us to characterize the degradation of a
transpressional segments of a left-lateral strike-slip system that is600 km long. Active reverse faults along the Gurvan Bogd rangecut through alluvial fans and terraces on the piedmont slope of
∗Now at: BRGM, dept. ARN, 3 ave Claude Guillemin, BP6009, 45060
the mountains. This is a general feature which is also observed in
Orleans, France. E-mail:
[email protected]
other places in Central Asia, for example in Southern Tibet and the
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
Figure 1. The Gurvan Bogd Range in the eastern Gobi Altai of Mongolia, showing our study locations.
Tien Shan (Tapponnier & Molnar 1979; Armijo et al. 1989; Avouac
example of variation of fault activity in time motivated us to study
et al. 1993; Molnar et al. 1994). Such reverse fault scarps located
the vertical slip rates in this particular area. Therefore, the fault
away from the main rangefront have been called "forebergs" (e.g.
scarps observed at the front of the Gurvan Bogd Range are par-
Bayasgalan et al. 1999a).
ticularly suitable for estimating deformation rate from morphology
The 1957 December 4 Gobi Altay earthquake (magnitude 8.3)
because they are well preserved. Indeed, the aridity, the lack of veg-
led to a 260 km left-lateral surface rupture and 100 km of surface
etation, the absence of human activity and the size of coseismic fault
rupture by reverse faulting along the Gurvan Bogd range (Kurushin
displacements (between 1 to 5 m of vertical offset along the Gurvan
et al. 1997). This earthquake was the focus of seismotectonic studies
Bulag thrust fault during a single earthquake in 1957, Fig. 1) allow
(e.g. Florensov & Solonenko 1963; Baljinnyam et al. 1993;
an unspoilt development of geomorphic markers that is not common
Bayarsayhan et al. 1996; Schwartz et al. 1996; Kurushin et al.
1997; Bayasgalan 1999; Bayasgalan et al. 1999a). Recent works
Only few studies have tackled the problem of morphological
(Bayasgalan et al. 1999a,b) investigated the relationships between
dating of cumulative reverse faults (Hanks et al. 1984, 1997;
the strike-slip faults and thrust faults in this region. Both are involved
Arrowsmith et al. 1996). Because the interactions between faulting
in rotations of crustal blocks about vertical axes, accommodating
history and erosion can be complex in such tectonic context, it is
SSW–NNE shortening due to the India–Eurasia collision. In this
necessary to identify from field observations the different processes
context, the thrust faults are directly involved in the recent uplift of
controlling the reverse faults scarps morphology. In this paper, we
the Gurvan Bogd mountains (Bayasgalan et al. 1999a,b; Owen et al.
first analyse the geomorphic relationships between alluvial sedi-
1999). Other studies were concerned with the climate-related allu-
mentation, erosion and faulting for some of the thrust fault scarps
vial fans cut by the faults along the Gurvan Bogd range (Ritz et al.
along the Gurvan Bogd range. This qualitative analysis is based on
1995; Owen et al. 1997; Carretier et al. 1998), and with the geomor-
descriptions of aerial photographs, precise GPS levelling of scarp
phic evolution of forebergs (Bayasgalan et al. 1999a). Bayasgalan
profiles and field observations. Then, we apply a simple scarp degra-
et al. (1999a) observed a wide range of reverse fault scarp mor-
dation model to several scarp profiles to estimate the morphological
phologies depending on their stages in development and their allu-
age of the deformation. This approach allows us to identify the dom-
vial environments. The evolution of thrust scarps into topographic
inant geomorphic processes and to test the limitation of our model
ridges seems to be related to fault geometry and the development
in each case. Finally, we compare our results with previous results
of backthrusts and folding (Bayasgalan et al. 1999a). In addition
concerning the seismic activity along the Gurvan Bogd range.
Owen et al. (1998, 1999) used arguments based on soil develop-ment and the dating of Quaternary sediments to propose that the
formation of alluvial fans at the foot of the Gurvan Bogd range is
mainly controlled by climatic variations. They identified the follow-
ing succession: 1) sedimentation under humid conditions dominated
In this section, the geomorphological evolution of reverse fault scarp
by perennial streams; 2) an increase in aridity causing a coating of
is considered by analysing the interactions between fan formation
coarse fanglomerates over the precedent fans by ephemeral streams
and thrusting for two reverse faults of the Gurvan Bogd range.
and the development of permafrost (22–15 ka); 3) the degradation ofthe permafrost and fan incision during early Holocene (13–10 ka).
2.1 The Gurvan Bulag fault (Figs 1 and 3)
According to Owen et al. (1999), deformation of fans by thrustingis contemporary with this last stage. Ritz et al. (1999) dated several
The Gurvan Bulag reverse fault scarp is 23 km long, with an E-W
alluvial surfaces along the Gurvan Bulag fault using cosmucleides
strike, and is roughly 5 km south of the foothills of Ih Bogd mas-
(Fig. 1). Their datings suggest that two major periods of alluviation
sif (Figs 1, 2a,c). The 1957 December 4 earthquake ruptured the
occurred at 118.6 ± 17.8 ka and at 12.7 ± 1.95 ka. The offsets of
entire length of the Gurvan Bulag scarp, producing 3–5 m high ver-
these alluvial surfaces lead to uplift rates at 0.18 ± 0.05 mm yr−1
tical offsets (Kurushin et al. 1997). Along the Gurvan Bulag fault
over the last 118.6 ± 17.8 ka, and 1.37 ± 0.25 mm yr−1 over the last
(Fig. 1), deformed zones by reverse faulting can vary even over a few
12.7 ± 1.95 ka. According to Ritz et al. (1999), the Gurvan Bulag
kilometres as illustrated by Fig. 3. This figure shows spot images
reverse fault evolved from a quiescent fault to a fault generating
of alluvial fans cut by the Gurvan Bulag reverse fault. In regions A
strong dislocations (∼4 m), separated by an interval of a few thou-
and C of Fig. 3 the fault scarp has reached a height of 100 m, asso-
sands of years (3.3 ± 1 ka). This interval is consistent with results
ciated with the development of a ridge. In region B in the front of
of palaeoseismological investigations (Bayasgalan et al. 1997). This
a main drainage basin outlet, the fault scarp is less developed. The
� 2002 RAS, GJI, 148, 256–277

Geophysical Journal International
S. Carretier et al.
Figure 2. Field photos. Triangles point the thrusts location. (a) View N of the Gurvan Bulag thrust, in front of a drainage basin outlet on the
southern side of Ih Bogd (site 1 on Fig. 1). (b) Preserved ridge of the Dalan Turuu Forberg on the northern side of Ih Bogd (site 4 on Fig. 1),
view S. (c) View E of the Gurvan Bulag cumulative thrust scarp (∼20 m high) (site 1 on Fig. 1). Note the frontal location of the 1957 scarp.
(d) Trench across the N-S cumulative thrust scarp at eastern end of Baga Bogd (site 3 on Fig. 1), view SW. The faulting has remained local-
ized at each event on a 45◦-dipping fault cutting the surface at the inflection point of the scarp profile (triangle). Dotted lines underline the unde-
formed stratification, showing that the scarp morphology is controlled by slope erosion and not by bending. E) View E of the cumulative thrust scarp
(∼20 m high) located SE of Baga Bogd (site 2 on Fig. 1). (f) Example of a cumulative reverse fault scarp morphology mainly controlled by internal structure
(Eggs mountains, site 5 on Fig. 1). (g) Example of cumulative reverse fault scarp (∼ 20 m) along the Gurvan Bulag foreberg, the form of which is mainly
controlled by gravitational processes. At this place, frontal collapse has reset most of the diffusive scarp from 1957 earthquake.
� 2002 RAS, GJI, 148, 256–277

Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
Figure 3. Stereo Spot images of the Gurvan Bulag thrust scarp (see Fig. 1 for location). This figure illustrates the differences in scarp morphology along the
thrust scarp. White lines underline the active streams flowing from the two main drainage basins. Dotted frames demarcates three regions where cumulative
scarps look clearly different. In frames A and C, away from the main drainage outlets, the thrust scarps correspond to well developed ridges ∼100 m high
associated with folding and backthrusting (Bayasgalan et al. 1999a). In frame B, in front of a main drainage outlet, the deformed alluvial fans look more linear,
without well developed ridge.
topographic ridges developed in regions A and C, are associated
The s4 surface corresponds to terraces inset in surface s3. Its
with pure reverse movement on the thrust and en ´echelon frac-
vertical offset along the fault is ∼6.5 m. The fact that it is located
tures and backthrusts which accommodate a strike-slip component
along the scarp suggests a tectonic origin. Ritz et al. (1999) dated
(Bayasgalan et al. 1999a).
this surface at 4.1 ± 0.7 ka.
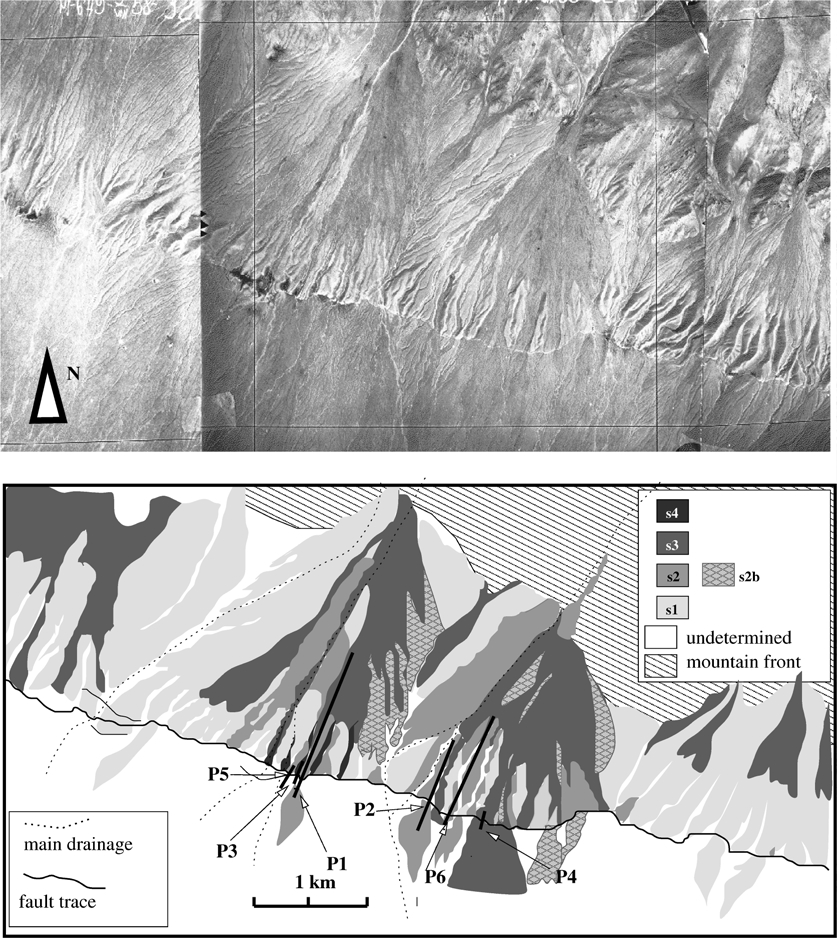
We used aerial photographs to identify four uplifted alluvial sur-
We levelled topographic profiles across these different uplifted
faces (s1 to s4, Fig. 4). We based our analysis on the density of
surfaces using differential GPS (Fig. 5). The repeatability in alti-
drainage networks and relative heights of terraces to give relative
tude is the order of centimetres. This is an acceptable precision
ages to the different surfaces (e.g. Bull & Pearthree 1988; Siame
to compare the profiles, considering that the scarp offsets exceed
et al. 1997). The oldest surface (s1) is incised by dendritic drainage
several metres.
networks. Where natural incision reveals a cross-section, it appears
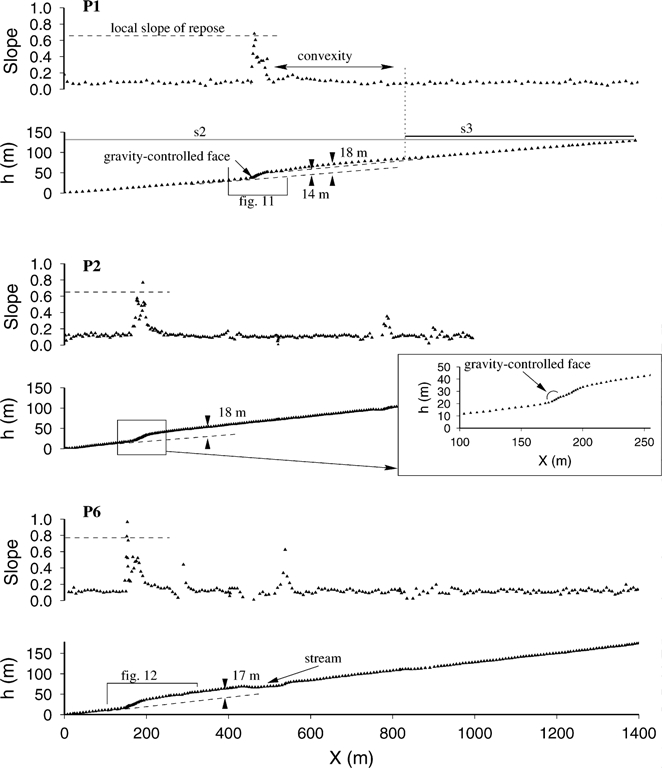
The gravity-controlled failure associated with the 1957 December
that this surface corresponds to alluvial deposits in which granite
4 event affected the fault scarp differently from place to place. On the
boulders typically 0.1–1.0 m in diameter can be found. These de-
profile P5 (Fig. 5), most of the scarp slope has been reset by gravity-
posits are deformed along the scarp, leading to a deeply incised
driven processes since the 1957 event. Consequently, if we measure
ridge, 500 m to 1 km wide and parallel to the thrust. In the central
the 1957 offset from the vertical height of the gravity-controlled
part of the Gurvan Bulag foreberg (Fig. 4) a large part of surface s1
face on the profile P5, we overestimate it (Fig. 5). On other profiles
has disappeared, removed by the two main outwash channels.
(e.g. P6 and P2, Fig. 5) the 1957 offset is localized at the base
The second surface (s2) is also incised by dentritic drainage net-
of the cumulative fault scarp, that allows the rest of the scarp to
works. It cuts into the surface s1 starting at the apex of the fans
be preserved from collapse. The preserved smooth morphology on
and forms terraces along the fault scarp. This s2 surface is mainly
scarp profiles P1, P2, P3 and P6 (Fig. 5) corresponds to the previous
visible within the central part of the region, in front of major out-
surface ruptures eroded by slope erosion. This suggests that faulting
wash systems (Fig. 4). This suggests a period of degradation after
steps forward in each event.
the deposition of s1, followed by the deposition of s2. The verti-
Scarp profiles P2 and P6 (Fig. 5) show constant slopes, whereas
cal offset of this s2 surface along the scarp is 17–20 m high. The
profile P1 levelled between regions A and B (Figs 3, 4 and 5)
age of this surface has been estimated from cosmogenic dating at
shows a convexity behind the frontal scarp. This convexity forms
118.6 ± 17.8 ka (Ritz et al. 1999). Some relics of the s2 surface
a ridge and drainage barrier at the western and eastern ends of the
(s2b) are sometimes difficult to differentiate from a younger surface
Gurvan Bulag foreberg. Where does this convexity come from and
s3 (Fig. 4).
what controls its amplitude? Bayasgalan et al. (1999a) pointed out
The s3 surface corresponds to debris flows. Its morphology is
the occurrence of both thrusts and backthrusts along the Gurvan
characterized by bars and swales, and rill-wash features. It covers
Bulag fault scarp. Although our profiles are not exactly at the same
a large part of the older fan surfaces north of the foreberg, which
places as Bayasgalan et al.'s observations, we interpret the convex-
provided a barrier to the sedimentation (Bayasgalan et al. 1999a).
ity shown on profile P1, as morphological consequences of folding
The thin coating of this deposit, made of coarse boulders typically
and backthrusting. This convexity is located between x ∼ 550 m
0.1–1.0 m in size, hampers its cartography. Consequently, some
and x ∼ 800 m on profile P1 (Fig. 5). The fault scarp is located near
portions of surface s3 that we reported on Fig. 4 may correspond
x ∼ 480 m. Between the fault scarp (x ∼ 480 m) and the beginning
to eroded older deposits (in particular s2b). Ritz et al. (1999) dated
of the convexity, the slope corresponds to the undeformed alluvial
surface s3 at 12.7 ± 1.95 ka. This age is consistent with an estimated
slope (Fig. 5). Consequently, it seems that the folding in this case
age of permafrost relics located around Artz Bogd (Fig. 1), which
is associated more with backthrusting than with the main thrust.
Owen et al. (1998) suggest corresponds to a Holocene transition
Profiles P3 and P4 have been levelled across less uplifted zones
from an arid and cold period to a warmer period.
(Figs 4 and 5). No clear folding appears on topography at this place.
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
S. Carretier et al.
Figure 4. Geomorphic analysis of aerial photos along the Gurvan Bulag foreberg, showing the locations of profiles used in Fig. 5. We identified several alluvial
surfaces from their relative elevation, and field observations. Surface s1 is the older and the more uplifted surface. Surface s2 corresponds to an alluvial fan
incased in s1. We interpret s2b as relics of surface s2 partially covered or washed by posterior alluvial deposits. Surface s3 corresponds to a thin alluvial deposits
incased of covering at some places s2. Surface s4 is the youngest surface, and it is located near the fault. Thick black lines indicate the location of topographic
profiles shown on Fig. 5. Solid lines show the location of scarp profiles (P1 to P6). These profiles were levelled in portions of scarp not altered by runoff driven
processes.
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
Figure 5. Elevation and slope profiles levelled across the Gurvan Bulag thrust (see Fig. 4 for localization). Note that on profile P5 the vertical height of the
gravity-controlled face greatly exceeds the value of the 1957 offset known at this place. Note also that on profile P1 the surface s3 stops at the onset of the
convexity that we interpret as a surficial effect of folding and backthrusting. On the contrary, profiles P2 and P6 show constant regional slope upwards from
the top of the scarp.
This suggests that folding grows in amplitude with the number of
of the convex ridge are drainage and sedimentation. On one hand,
events and when backthrusting has taken place. However, we do
the convex ridge developed in the oldest surface s1 disappears in the
not have any trench evidence that no folding occurred at this place
central part of Gurvan Bulag, in the front of the two main drainage
in relation with the main thrust. In some other places along the
basins, which have presumably eroded it away during periods of
Gurvan Bogd range, trenches show a simple reverse fault cutting
high fluvial transport (see frame B of Fig. 3). On the other hand,
through undeformed sediments (for example, see Fig. 2d). Other
where the ridge acts as a barrier, sedimentation which accumulates
examples show that a part of the fault scarp is controlled by bending
behind it also tends to level the convexity. By successive alluvial
(for example, see Fig. 2f). Consequently, folding is not a general
filling, the convexity tends to disappear by burial. On the profile P1
feature in this area. When it develops, it can cause the scarp to
(Fig. 5), the alluvial fan s3 stops against the convexity developed in
appear older, because it gives an apparent eroded shape upwards
s2. This effect explains why profiles P2 and P6 look roughly linear
(Fig. 2f). This should strongly limit the morphological dating of
(Fig. 5). The area in front of the main drainage basins is also one
such scarps. We will evaluate this effect from the analysis of scarp
of abundant alluvial supply. Despite the linear fan shape observed
profiles in a next Section. The other main controls on the amplitude
on profiles P2 and P6 levelled on the surface s2, this surface is
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
S. Carretier et al.
Figure 5. (Continued.)
probably not all of one age between the fan apex and the fault scarp
(s2) has an intermediate character between dendritic incision and
bar-and-swales. The presence of this surface within the apex of s1suggests that it formed during an aggradation period and is thus afan surface (Fig. 6). Surface s2 is also affected by the thrust. The
2.2 E–W thrust scarp to the south of Baga Bogd
most recent surface (s3) has a bar-and-swales character and corre-
(Figs 1 and 6)
sponds also to an alluvial surface. This surface has not been uplifted
We identified four geomorphic surfaces at this place (s1, s1b, s2,
(Fig. 6). Consequently, the thrusting activity on this scarp occurred
s3) (Fig. 6). These surfaces were not cut by thrusting in the 1957
before the deposition of s3 and stopped between the depositions of
earthquake (Florensov & Solonenko 1963). The oldest one (s1) is
s2 and s3. However, we do not have dating information for these
incised by dendritic drainage networks and is the highest recogniz-
surfaces. So, although surface s3 at this location has the same geo-
able surface uplifted by the reverse fault. Natural incision reveals
morphic features as surface s3 at the Gurvan Bulag fault (dated at
that this surface corresponds to alluvial deposits in which granite
12.7 ± 1.95 ka), we can not prove that these surfaces are the same
boulders typically 0.1–1.0 m in diameter can be found. The second
surface (s1b), uplifted ∼15 m by the thrust, is embedded in s1. We
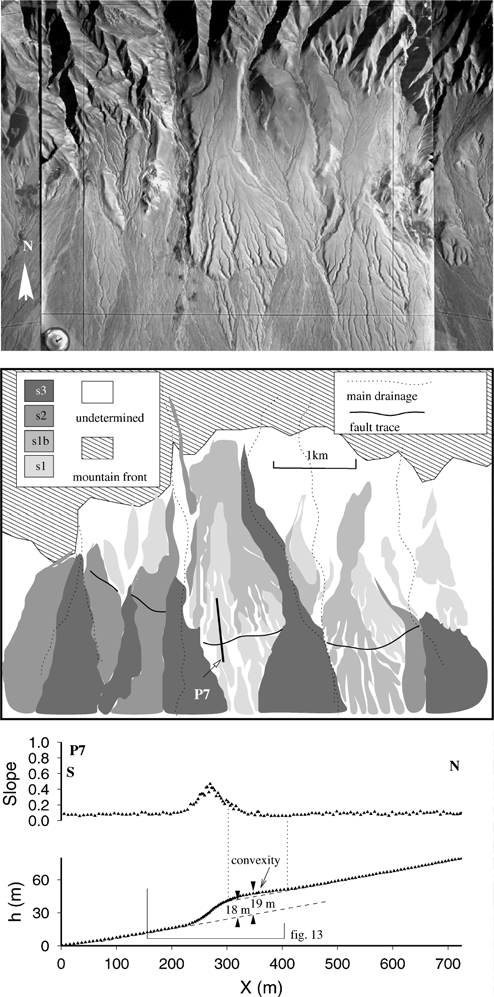
The scarp profile P7 presented in Fig. 6 was obtained on sur-
interpret s1b as a wash surface, probably corresponding to a hu-
face s1, uplifted between 18 m and 19 m at this place. This pro-
mid pulse during the early history of the uplift. The third surface
file was levelled in a portion of the scarp preserved from runoff
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
Figure 6. Geomorphic analysis of aerial photos along the thrust SE of Baga Bogd (see Fig. 1 for location). We identified 4 alluvial surfaces from their relative
elevation and field observations. The oldest and more uplifted surface s1 corresponds to a debris flow surface. Surface s1b is embedded in s1 and we interpret is
as a wash surface. Surface s2 correspond also to a debris flow surface embedded in s1 and s1b. Surface s3 corresponds to the youngest deposit and is unaffected
by the thrust, showing that this fault has not broken the surface from the deposition of s3. The black line indicates the location of the scarp profile P7. This
profile was levelled in a portion of scarp not altered by runoff driven processes. Elevation profile shows a convexity at the top of the scarp which is interpreted
as morphological effect of folding. The maximum cumulative offset including the folding component is 19 m. The cumulative offset associated with faulting
only is ≤18 m.
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
S. Carretier et al.
processes. Profile P7 has a roughly symmetric shape that we do not
from the upstream fan sources. We will focus our study on portions
observe on profiles levelled along the Gurvan Bulag thrust scarp
located between incisions, where surfaces have been preserved from
(see also the field photograph, Fig. 2e). This morphology can be
runoff processes by their offset. In these portions, the fault scarps are
explained by a fixed fault cutting the surface at the inflection point
eroded only by slope processes which are the only processes taken
of the elevation profile. A convexity appears on the elevation pro-
into account in our modelling approach. We took profiles far enough
file between x ∼290 m and x ∼ 400 m (Fig. 6). This convexity is
from drainages to ensure that main gradient is oriented normal to
interpreted as a morphological consequence of folding. No obvi-
the fault, so that 1-D modelling can adequately reproduce the main
ous surficial trace of a backthrust can be observed in association
direction of sediment flux. We attempt to interpret the discrepancies
with this convexity, but it may have disappeared by erosion from
between our model and the data according to the influence of other
the cessation of the seismic activity. Because of the folding compo-
geomorphic processes that we can identify.
nent of the offset, the slope profile shows two populations, separatedat x ∼ 290 m (Fig. 6). Unlike our interpretation along the Gurvan
Bulag fault scarp, these two populations do not correspond to vari-able locations of the fault responsible for the surface rupture. The
Four approaches are possible to model the evolution of scarp mor-
maximum cumulative offset including the folding component of
phology on active faults: 1) the scarp morphology is assumed to be
the uplift is estimated at 19 m (Fig. 6). The cumulative offset cor-
controlled by elastic displacements of the surface related to dislo-
responding to the approximation of the hangingwall surface by a
cation at depth (e.g. King et al. 1988; Stein et al. 1988; Taboada
planar surface is 18 m (Fig. 6). This offset is an estimate of the
et al. 1993); 2) the scarp is assumed to be controlled by surface
uplift component due to faulting only.
rupture and slope erosion processes (e.g. Culling 1960; Nash 1981;Avouac 1993; Arrowsmith et al. 1998); 3) the scarp evolution iscontrolled by both effects 1 and 2 (e.g. Arrowsmith et al. 1996); 4)
2.3 General implications for the morphological evolution
the scarp morphology is assumed to be controlled by slip between
of forebergs
stratified deposits of different rheology (Nino et al. 1998). We chose
The observed variability of topographic expression associated with
the second approach which involves imposing the surface rupture
reverse faulting seems to be related to cessation of alluvial depo-
and modelling the erosion of scarps using a linear diffusive ana-
sition and evolution of the fault system itself. The repetition of
logue. We did this for several reasons: 1) our goal is to date scarps
earthquakes increases the surface deformation, so that the thrust
using the erosion of their morphology; 2) elastic dislocation models
scarp eventually forms a topographic ridge, which can act as a bar-
are very sensitive to the fault geometry and depth (King et al. 1988;
rier to sedimentation (Fig. 7a). However, for a scarp to achieve this
Arrowsmith et al. 1996), which are not well constrained in our area.
morphology it must be located either far from outwash channels
Therefore, the width of our topographic profiles is short (several
of major drainage basins, or to the side of them. When the thrust
100 m) compared to the length of the faults (10–20 km), so the ef-
scarp is close to and in front of a major drainage basin outlet it is
fect of the elastic dislocation modelling is diminished (Arrowsmith
modified by processes including scarp abrasion and deposition, de-
et al. 1996); 3) scarp morphology depends on interactions between
pending on the fluvial transport capacity and the sediment supply in
successive alluvial deposits and the seismic cycle. In most of the
the drainage basin (Carretier et al. 1998). These alluvial processes
cases we discuss, uplifted and preserved surfaces do not correspond
can cause destruction of the scarp or filling of the depression be-
to single surfaces that can be modelled by an elastic dislocation
tween the remnant scarp convexity and the range front (Fig. 7b),
and may be influenced by climatic variations. The resulting uplifted
Morphological dating is the process of comparing modelled and
alluvial surfaces can be flat (see profile P2, Fig. 5). Consequently,
observed profiles to determine the age of the landform. We use
when the thrust scarp is far from main drainage basin, the wave-
a linear diffusion analogue to describe scarp erosion preserved
length of the deformation associated with thrusting is revealed by
from runoff processes (portions of fault scarps located between
the distance between the scarp front and the toe of the alluvial de-
incisions). In this case, the transport law is that the local flux of
posits (Fig. 7a). However, when the scarp is in front of a main basin
sediments is proportional to the local topographic slope (Culling
outlet, the distance between the thrust front and the alluvial deposits
1960). We assume that material of faulted alluvial fan has been al-
is controlled instead by successive erosion and deposition horizons
ways available for transport. This is consistent with non-cohesive
(Fig. 7a). In principle, the wavelength over which incised channels
alluvial sediments observed on the field. Thus, assumption of trans-
and terraces form is also influenced by the down-dip fault length,
port limited conditions and application of the continuity equation
as shown in numerical models of elastic displacement fields and
for sediment flux will result in a diffusion-like equation relating the
diffusive geomorphic processes (Arrowsmith et al. 1996). In prac-
local erosion rate and the local topographic curvature ( ∂h = κ ∂2h
tice, the real wavelength of the deformation appears to be controlled
where h iselevation at point x, and t the time). The proportionality
by the location of backthrusts, which may correspond to a flatten-
coefficient κ [in unit of m2 ka−1] is called the diffusion coefficient.
ing of the thrust dip at depth (Fig. 7). The variation in apparent
By fitting synthetic topographic profiles computed with these as-
wavelength along the Gurvan Bulag foreberg ridge is more likely
sumptions to observed scarp profiles we can estimate the product
to be controlled by the scarp location relative to the main drainage
κt where t is the age of the scarp. We will call this product the
basins than by lateral variations in fault dip. The scarp of Dalan
"morphological age" of a scarp.
Turuu, north of Ih Bogd, illustrates this conclusion (Figs 1 and 2b).
Dating scarps becomes more uncertain when repeated faulting is
This thrust scarp forms a topographic ridge 200–300 m high, with
involved, as Avouac & Peltzer (1993) show for cumulative normal
a constant width along the fault. No major drainage basin crosses
fault scarps. In this case the unknown parameters controlling erosion
and tectonics are multiplied by the number of events. This is even
In the second part of this study, we will model scarp profiles to es-
more difficult in the case of cumulative reverse faults because of
timate their morphological ages. These scarps are incised by locally-
the variability of the surface faulting itself. Numerous descriptions
formed drainages and also thorough-going or antecedent drainages
of trenches across reverse active faults show that the position of the
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
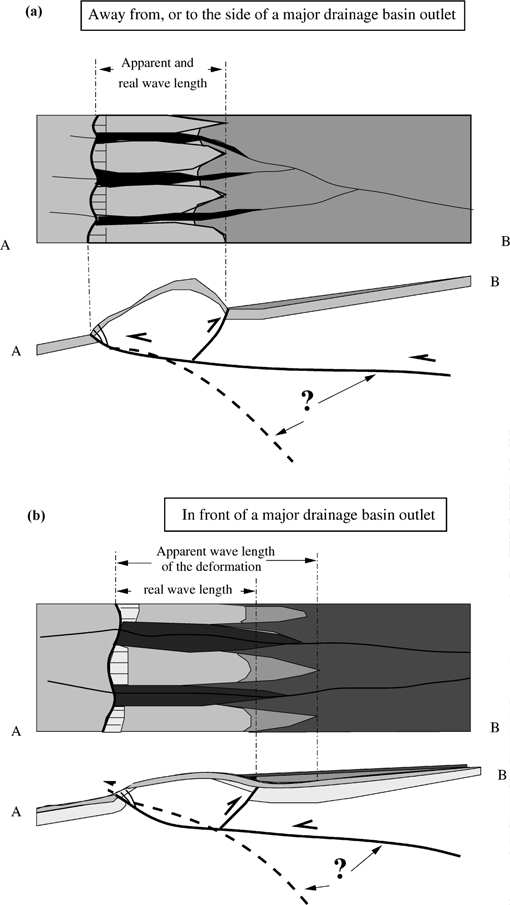
Figure 7. Conceptual sketches that illustrate alluvial sedimentation contexts and foreberg morphologies. (a) When the foreberg is away from a major drainage
basin outlet, the geomorphic limit between alluvial surfaces is mainly controlled by the development of a folded and backthrust ridge that forms a barrier to
sedimentation. In this last case, the distance between the fault trace and the lower limit of recent fans shows the true wavelength associated with the folding
and backthrusting. (b) However, when the foreberg is located in front of a major drainage basin outlet, the fluvial transport (abrasion or sedimentation) tends
to level the regional scarp slopes. Limits between alluvial geomorphic surfaces in map view are mainly due to the interplay between stream incision and the
development of terraces rather than the surface displacement due to folding and backthrusting.
rupture at each event is usually variable, unlike most cases of normal
suggest that the rupture steps forward in each event (Figs 2 and 5).
faulting (see for example McCalpin, 1996, pp. 107–211; Meghraoui
Hanks et al. (1984) proposed a simple analytical model for dat-
et al. 1988; Swan 1988; Philip et al. 1992; Yeats et al. 1997,
ing cumulative scarps, involving diffusion of continuous uplift on
p. 352). Along the Gurvan Bulag ranges, the position of the 1957
a fixed and vertical fault. His model cannot be applicable in such
event trace at the base of cumulative scarps and trench observations
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
S. Carretier et al.
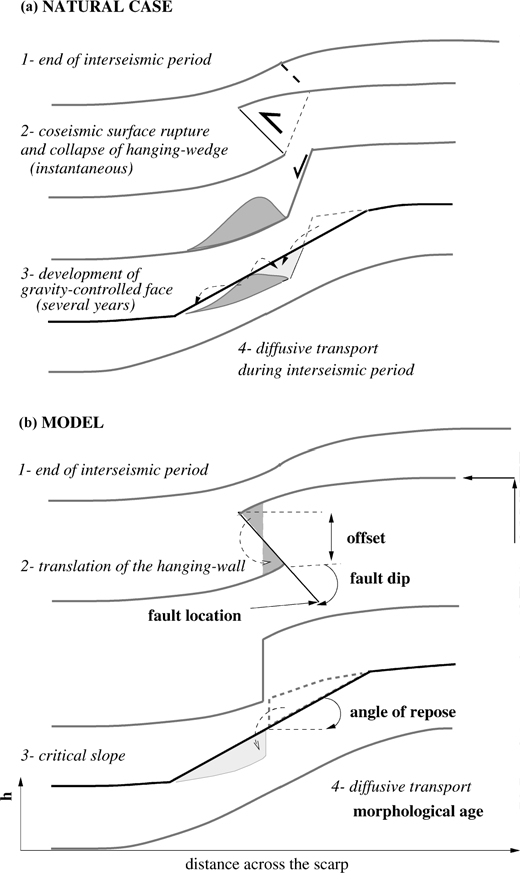
Figure 8. Modelling of reverse faulting and scarp erosion. (a) Natural case. Three stages can define the geomorphic evolution of a reverse fault scarp:
(1) instantaneous collapse of the hanging wedge due to reverse movement, (2) development of a gravity-controlled face at the angle of repose of the material
over several years. At the end of this stage, material is equally distributed between hangingwall and footwall. 3) Diffusive transport. (b) Model. The surface
rupture is modelled by a translation of the profile in the hangingwall according to specified dip of fault and vertical offset and from the middle of the hanging-
wedge. The gravitational collapse is modelled by reducing all slopes greater than the specified slope of repose. These two steps preserve the mass-balance
between hangingwall and footwall. Linear diffusion is then applied during a specified morphologic duration (K �t).
We thus introduced some extra complications in our model al-
model used by Avouac & Peltzer (1993) for cumulative normal fault
lowing the position of each rupture, which can be variable in each
scarps. Gravity-controlled failure of scarps has been well described
event, and the fault dip at the surface to be specified (Fig. 8).
and is common when faulting occurs in non-cohesive material
We also allow the surface slope to collapse after a surface rup-
(Wallace 1977; Machette 1987) leading over several years to
ture when the slope exceeds the slope angle of repose of the
a gravity-controlled face that forms after the collapse of the
non-cohesive material. In that sense, our model is similar to the
hangingwall-wedge by a normal fault whose position can be
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
variable (McCalpin 1996, p. 200) (Fig. 8a). The gravitational col-
lapse is not a diffusive process. It is driven by internal friction ofunconsolidated material (Roering et al. 1999). Thus, when the scarp
Fig. 9 illustrates schematically two extreme cases observed in our
slope reaches a threshold slope (or "slope of repose"), it collapses
numerical experiments. They differ by the relative magnitude of
quickly. We observed that this process is a strong controlling factor
parameters. The inherited diffusive scarp morphology may or may
of scarp evolution. For example, Fig. 2A and profile P5 (Fig. 5)
not be preserved when a new seismic event occurs. This depends
show a cumulative reverse fault scarp for which the frontal portion
on gravity-driven processes that tend to maintain scarp slopes at
collapsed during the 1957 event. This process affected a large part
the angle of repose of detritic material, resetting the diffusive scarp
of the scarp, which consequently lost its diffusive morphology. The
morphology. In terms of morphological dating, such resetting is
resulting gravity-controlled face will then erode by diffusion until
equivalent to resetting the clock. Indeed, large offsets and repeated
the next surface rupture. The future diffusive morphology will only
surface rupture at the same place (Fig. 9, case A) enhance the de-
provide information about the age of the 1957 event. Consequently,
velopment of a gravity-controlled face. In this case, the gravity-
it is clear that this process is a strong limitation for dating of the initi-
controlled height exceeds the true value of the vertical component
ation of uplift. Along the Gurvan Bulag range, the vertical height of
associated with a single surface rupture. As mentioned previously,
the gravity-controlled face acquired several months after the 1957
such behaviour has been observed along the Gurvan Bulag range
dislocation is variable, even between places separated by only a few
(see Fig. 2a and profile P5 on Fig. 5). This effect can have important
hundred of metres (compare for example profiles P5 and P2, Fig. 5).
implications in palaeoseismology, as well as for scarp morphology
These observations show that slope collapse can refresh reverse fault
and dating. When estimating the vertical component of a surface
scarp morphology to varying degrees, and consequently it must be
rupture from the total vertical height of the gravity-controlled face,
taken into account in our morphologic dating model. Some authors
this effect will lead to an overestimate of the last vertical offset. This
used forward modelling in which gravitational collapse is computed
suggests that 1957 offsets along the Gurvan Bulag range could have
at the same time as diffusion (e.g. Arrowsmith et al. 1998). This is
been overestimated by Kurushin et al. (1997) when using height
very useful to estimate slip rates when processes are demonstra-
of the gravity-controlled face (e.g. Kurushin et al. 1997 site 17,
tively continuous. In the case of repeated faulting with large offsets,
p. 99), and some cumulative scarps considered previously as one
the possible variation of the surface rupture location and the vari-
event scarp could be in fact two-events scarps (see for example pro-
able degree of frontal collapse impose to respect the succession of
file P4 in Fig. 5). By contrast, distinct forward-stepping faults with
small offsets preserve the diffusive scarp morphology (Fig. 9, case
In summary, we model topographic scarp profiles as follows
B). Between these two extremes cases, we obtained a lot of differ-
ent morphologies which can not be summed up in a general graph.
These morphologies differ by their relative record of past events.
(i) we chose the position of the surface rupture and of the dip of
Thus, preservation of diffusive morphology depends on local fac-
tors which must be evaluated in the field and by modelling.
(ii) we specify the offset on the fault;
Consequently, it is clear that dating the beginning of the ramp
(iii) we simulate the initial collapse of the hangingwall by form-
formation is not always possible. In the worst cases, we can only
ing a vertical step in the middle of the offset (Fig. 8b). This choice
date the penultimate event (in this case, the event before 1957).
allows to preserve the mass-balance between eroded material from
For example, our theoretical simulations of ruptures localized on
the hangingwall and the deposited sediment in the footwall at the
a 45◦ dipping fault suggest that incremental offsets greater than
end of the next modelling step, whatever the position of the nor-
3 m will imply a total resetting of the diffusive scarp at each event,
mal fault is, until its dip is greater than the critical slope (Fig. 8b).
whatever values the other parameters have. This is in contrast to
This modelling preserves the shortening associated with the reverse
the case of repeated normal faulting. Although development of a
gravity-controlled face can occur in both cases, in normal faulting
(iv) We allow the slope to collapse under gravity in order to bring
the increase of the scarp length (distance between two symmetrical
the scarp slope to the angle of repose of the material (∼30◦). To
points in the hangingwall and in the footwall) preserves diffusive
achieve this we apply diffusion with very high diffusion coefficient
scarp morphology.
to slopes exceeding the slope of repose (Andrews & Hanks 1985).
Although gravitational collapse is not a diffusive process, this nu-merical method enables to respect mass balance of transport. It also
enables us to reduce slope instantaneously by using a sufficiently
high diffusion coefficient. The transport-limited condition implies
In order to determine the best fitting values of morphological age
that this process affects all slopes greater than the angle of repose,
for the different processes, we performed a parameter search by
and thus that the free face formed just after the earthquake is very
forward modelling in which κ�t (product of diffusion coefficient
quickly degraded. This is consistent with our field observations.
and interseismic duration) is incremented, and for each value the root
(v) A linear diffusion equation is then solved by "forward time
mean square of the misfit between observed and modelled elevation
central space" finite difference method over the imposed duration
profiles is calculated (Avouac 1993; Arrowsmith et al. 1998):
of the interseismic period (�t).
Synthetic cumulative scarps profiles are calculated by repeating
(hmodelled(x j ) − hobserved(x j ))2
these four stages. For each time period, defined by either tectonic
displacement, gravitational collapse or diffusive erosion, we canimpose the values of vertical offset, fault dip and position, slope
where n is the number of points x j of the observed profile.
angle of repose, diffusion coefficient and duration between events
The RMS versus κ�t passes through a minimum RMSmin which
(both included in the term κ�t).
corresponds to the best fitting κ�t. In order to estimate a confidence
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
S. Carretier et al.
Figure 9. Schematic results of numerical modelling for two extreme cases. In case A the reverse component of faulting removes a part of inherited diffusive
morphology at each event so that gravity-driven collapse of slope after each surface rupture resets the diffusive fault scarp morphology. Repeated localization of
the rupture in the same place and high incremental offsets enhance this effect. Consequently, the vertical height of the gravity-controlled face exceeds the value
of the incremental offset. In case B, forward stepping of successive dipping faults and low incremental offsets values preserve the diffusive scarp morphology.
interval of the inferred age, we related the range of acceptable fit-
GPS method which is accurate to less that 5 cm. Consequently, this
tings to the RMS values lower than RMSmin + 5 cm. By doing this,
value is adapted to define confidence intervals of morphological
we retained the same criterion proposed by Avouac (1993) and used
ages estimated in this study. This criterion allows us to determine
by other authors (e.g. Avouac & Peltzer 1993; Arrowsmith et al.
the values κ�tmin and κ�tmax corresponding to values of κ�t at the
1998). This criterion has been used to determine an objective es-
intersections between the RMS curve and the horizontal line defined
timation of the precision with which morphological ages are esti-
by RMS = RMSmin + 5 cm. We define the morphological age by
mated, taking into account topographic levelling with precision of
κ�tmin+κ�tmax and its uncertainty by κ�t
max minus the morphological
about 5 cm. In that sense, if several models can match the same data
age. When converting morphological ages into diffusion coefficient,
with RMS lower than RMSmin + 5 cm, they will not be differen-
we propagate the uncertainty associated with each parameter as fol-
tiated. The levelling of our profiles has been made by differential
lows: considering that δκt and δt are the uncertainties associated
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
with values of κt and t respectively, then κ is given by κt ± δκ,
scarp would be lower than the slope of repose of the material, espe-
where δκ is
κ )2 + ( δt )2 (Bevington & Robinson 1992). We ap-
cially in the case of one event scarps. Nevertheless, all our profiles
ply the same method to convert morphological ages into numerical
display a slope at the front of the scarp (∼0.7) which corresponds
ages or slip rates.
to classical values for slope of repose of detritical sediments (e.g.
Morphological age is not the only parameter which controls the
Wallace 1977; Machette 1987; Avouac & Peltzer 1993) (Fig. 5).
accuracy of fittings between observed and modelled profiles. The
Although this hypothesis can not be rejected by direct evidence,
determination of the best fitting morphological age and uncertainty
morphological arguments seem to favour the stepping of successive
requires estimation of several parameters such as number of events,
the incremental offsets, the dip of the faults, their location, the angle
To determine the location of the successive faults responsible
of repose of material, and the regional (initial) slope of the profile.
for the surface rupture requires one to look at slope profiles. A
Some of these parameters can be evaluated from field data, namely
surface rupture associated with a seismic event causes an abrupt
the regional slope corresponding to the portion of profile far from
perturbation of the slope profile. When a surface rupture is followed
the scarp, and the angle of repose which is given by the portion
by an interseismic period this perturbation acquires a "Gaussian"
of the scarp associated with the 1957 event. Other parameters are
shape, that is predicted by a diffusion model (Fig. 9 case A, slope
more difficult to determine. For example, the dip of the faults and
profile) (Avouac 1993; Nivi ere et al. 1998). Assuming that their
their location remained uncertain in most of the cases. A trench
formation is only related to surface rupture, the identification of
across a fault scarp, which is necessary to determine the fault ge-
these "Gaussians" or inflections of a slope profile depends on the
ometry, has not always been possible, especially when scarps are
distance between the successive surface ruptures (compare Fig. 9
several metres high. Consequently, the solution given for each mod-
case A and case B). Consequently, we can estimate the location of
elled profile should not be unique. Therefore, estimated morpholog-
the successive faults from the slope profile independently of the
ical ages and their uncertainty should depend on the assumptions
morphological age, in such a way that the locations of observed and
made about fault geometry, values of incremental offsets and num-
modelled slope inflections fit.
ber of events. Keeping this in mind, we fix these parameters using
The dip of faults is one of the parameters controlling the grav-
morphological arguments, and compare our results with previous
itational collapse of the scarp, and thus the preservation of the
estimations of slip rates and time recurrence intervals based on cos-
diffusive scarp morphology (Fig. 9). This parameter cannot be eval-
mogenic dating of uplifted surfaces in our study site (Ritz et al.
uated in this study. However the estimation of the best fitting mor-
phological age does not depend on this parameter when the mor-
We assume that the interseismic duration �t and the diffusion
phology associated to past events is preserved (see Appendix A,
coefficient κ are constant, so that RMS is computed with constant
Figs A1a,b).
κ�t. As Arrowsmith et al. (1998) as well as others showed (e.g.
The successive steps of our fitting method are the following:
Nivi ere & Marquis 2000), the uncertainty of morphological ageincreases with the age of the scarp. Consequently, the single value
(i) The incremental offset and the number of events are estimated
of κ�t relative to a past event can not be resolved with a good
from the elevation profile, and the slope of repose and the regional
accuracy (see Appendix A, Fig. A1c). On the contrary, constant
slope are estimated from the slope profile. The slope of repose is
κ�t between events allows us to estimate a best fitting value with a
estimated from the mean slope of the gravity-controlled face rather
good accuracy (see Appendix A, Fig. A1c). The best fitting value of
than local maximum.
κ�t that we compute has consequently the sense of a mean value,
(ii) The successive fault locations are estimated from the slope
which gives mean dating and uplift rate.
profile. The fault dip is taken arbitrary lower than vertical (50◦) to
We assume that the incremental offsets are equal to the local
reduce the uncertainty of the best fitting morphological age (see
value associated with the 1957 event (Kurushin et al. 1997), and
Appendix A).
in this sense the successive events are "characteristic" as suggested
(iii) Forward modelling assuming non-vertical faults is carried
by Ritz et al. (1999) and Kurushin et al. (1997). Consequently, to
out to evaluate if the scarp could have been reset during the uplift.
estimate the number of events, we divided the cumulative offset by
This step aims at determining whether the initiation of the uplift or
this incremental offset.
only the last events can be dated (see Fig. 9).
We assume that the fault responsible for the surface ruptures
(iv) The RMS is calculated for different values of κ�t and the
steps forward at each event. We have no direct evidence of this
best fitting morphological age and its associated uncertainty is de-
behaviour for the studied profiles because it has been impossi-
ble to trench across scarps which can reach 20 m height. How-
We apply this methodology to the examples previously described.
ever, some other trenches across reverse fault scarps around the
In each case, the RMS between observed and modelled profiles is
Gurvan Bogd range displayed such pattern, while some other showed
computed only on the apparent diffusive portion of the scarp.
unique faults or more complex geometry (Bayasgalan et al. 1997;Bayasgalan 1999). We argue for a forward stepping of the faultsfrom the scarp morphology: first, the portion of the scarp associated
E X A M P L E S
with the more recent event (1957) is generally located at the front ofscarps (Fig. 5); secondly, slope distribution across scarps is usually
6.1 The Gurvan Bulag reverse fault (Figs 1, 3 and 4)
not symmetrical, and slope decreases upwards from the position ofthe last rupture (Fig. 5). This suggests that the upper part of scarps
As mentioned earlier, cosmogenic dating of uplifted alluvial fans
is more degraded and thus older than the lower one. Such morphol-
allowed Ritz et al. (1999) to propose that seismic activity resumed
ogy may also result from the ridding of the hangingwall over the
on this fault from at least the deposition of surface s3 dated at
land surface by the way of a flat fault, prolongating a shallow ramp
12.7 ± 1.95 ka. By the morphological dating of cumulative reverse
fault geometry. In this case, the frontal part of the scarp would cor-
fault scarps, we want to date the beginning of the uplift of the older
respond to the propagating flat fault. Thus, the slope of the frontal
surface s2 (deposition at 118.6 ± 17.8 ka, Ritz et al. 1999).
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
S. Carretier et al.
Figure 10. Morphological dating from Profile P3 (see Fig. 4 for location). Triangles are data and solid lines are models for the best fitting morphological age,
using two events of 3.2 m offset on faults dipping 50◦ with 10 m distance between the two slip surfaces. The best fitting morphological age and associated
uncertainty is determined graphically from the RMS versus constant κ�t. The RMS is calculated from the elevation data, over the length corresponding to the
diffusive morphology (horizontal arrow on the elevation profile). To define the range of acceptable values of κ�t, we retain all models for which the RMS lies
between RMSmax and RMSmin +5 cm (see text for details).
6.1.1 Profile P3 (Figs 4 and 10)
15 m and 12 m stepping of the successive faults (dipping at 50◦) re-sponsible for the surface ruptures, we estimate a mean κ�t ranging
This profile is levelled across surface s4, uplifted 6.5 m (Fig. 10).
from 6.5 m2 to 19 m2 from the RMS curve (κ�t = 12.75 ± 6.2 m2)
This cumulative offset is twice the vertical offset of the 1957 event
(Fig. 11). This result is fairly consistent with the last morphologi-
(3.25 m). The gravity-controlled face associated with the 1957 event
cal interseismic duration κ�t calculated from profile P3 (Fig. 10).
is located at the front of the scarp, allowing to preserve the diffusive
The mean value of the morphological age at the profile P1 loca-
morphology associated with the last interseismic period. Using two
tion (three interseismic periods) is 38.25 ± 18.6 m2. If we use the
events (including the 1957 event), with faults dipping 50◦ and 10 m
coefficient of diffusion calibrated from the profile P3, we date the
apart, morphological ages determined from the RMS range fromκ�
initiation of the uplift responsible of the cumulative offset of sur-
t = 7 to 20 m2 (Fig. 10). The mean morphological age of the
face s2 at 11.7 ± 8.1 ka, and the penultimate event at 3.9 ± 2.7 ka.
penultimate event is thus 13.5 ± 6.5 m2. Ritz et al. (1999) estimated
These estimates are consistent with 10Be dates (Ritz et al. 1999)
the age of the uplifted surface s4 at this place to be 4.1 ± 0.7 ka,
as well as with preliminary results from palaeoseismological inves-
based on cosmogenic measurements. It allows us to calibrate the
tigations giving the penultimate event at ∼4 ka (Schwartz et al.
coefficient of diffusion κ in our model at κ = 3.3 ± 1.7 m2 ka−1,
1996; Bayasgalan et al. 1997). The uplifted surface s2 being dated
close to other estimates in the same climatic conditions (for example
at 118.6 ± 17.8 ka (Ritz et al. 1999), these results confirm that the
in the Dsungar desert located in Central Asia; Avouac & Peltzer
seismic activity on the Gurvan Bulag fault resumed at ∼12 ka, and
1993; Hanks 1999).
consequently, that this fault was almost quiescent between ∼118 kaand ∼12 ka. Over the last 11.7 ± 8.1 ka, we estimate from the 14 mcumulative offset of s2 an uplift rate on the Gurvan Bulag fault at
6.1.2 Profile P1 (Figs 4 and 11)
1.2 ± 0.8 mm yr−1. This value is consistent with the previous es-
This profile is levelled across surface s2, uplifted between 14 m and
timate at 1.37 ± 0.25 mm yr−1 given by Ritz et al. (1999) for the
18 m (Figs 4 and 5). The gravity-controlled face is localized at the
same duration.
base of the scarp and most of the inherited diffusive morphologyis preserved, allowing us to estimate the morphological age of the
6.1.3 Profile P6 (Figs 4 and 12)
cumulative uplift (Fig. 9, case B). We identified on profile P1 thefolding component of the uplift, which seems to not affect the slopes
This profile is levelled across surface s2, uplifted 17 m, in front of
near the fault scarp (Fig. 5). Thus, we will estimate the morpholog-
a major drainage basin (Figs 4 and 12). Just as we detected 4 events
ical age of the scarp from the data located in the region presumably
on profile P1 responsible for the uplift the surface s2, we mod-
undeformed by folding (x < 520 m, Figs 5 and 11). The correspond-
elled the cumulative offset on profile P6 also using 4 events, with
ing cumulative offset (14 m) is four times the local vertical offset
vertical incremental offsets of 4.25 m. The 1957 gravity-controlled
associated with the 1957 event (∼3.5 m) (Fig. 11). The decreasing
face is located at the base of the scarp, suggesting a forward step-
slope from the bottom to the top of the scarp and the frontal loca-
ping of the fault. The slope profile shows a peak corresponding to
tion of the gravity-controlled face suggest that the rupture stepped
the gravity-controlled face, followed by a roughly gaussian shape.
forward (Fig. 11). Using 4 events with 3.5 m offsets, and 15 m,
Our numerical experiments suggest that the fault scarp collapsed
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
Figure 11. Morphological dating from profile P1 (see Fig. 4 for location). Triangles are data and solid lines are models for the best fitting morphological age,
using four events of 3.5 m offsets on faults dipping at 50◦, with 15 m, 15 m and 12 m distance between successive slip surfaces. The best fitting morphological
age and associated uncertainty is determined graphically from the RMS versus constant κ�t. The RMS is calculated from the elevation data, over the length
corresponding to the diffusive morphology (horizontal arrow on the elevation profile). To define the range of acceptable values of κ�t, we retain all models for
which the RMS lies between RMSmin and RMSmin +5 cm (see text for details).
between each event prior to 1957. Coseismic scarp resetting occurs
for P3). It is difficult to evaluate the contribution of folding to the
at each event because of the high offsets and because the fault steps
cumulative offset on P6, because this folding is masked by alluvial
at this locality (adjusted to fit the locations of inflexions on the slope
sedimentation, that leads to a constant slope in the hangingwall.
profile) is smaller than at the location of profile P1 (Fig. 11). This
However, the cumulative offset estimated from profile P6 is similar
occurs if we consider either faults dipping at 50◦ or vertical faults.
to the maximum cumulative offset given by profile P1 (18 m). The
Only the 1957 event allowed to preserve remaining diffusive mor-
maximum offset on P1 includes the folding component of the up-
phology because it is located far from the penultimate rupture. This
lift, which appears more clearly than for profile P6. If our estimates
suggests that the remaining diffusive morphology has developed
of offsets are higher than the real ones, we will overestimate the
from the penultimate event, from a stage where the scarp was domi-
morphological age (for two scarps with different offsets but with
nated by the stable gravity-controlled slope. Consequently, from the
identical degradation states, the diffusion model will predict higher
profile P6 we can estimate only the value of κ�t corresponding to
κ�t for the greater offset).
the duration between the penultimate event and the 1957 event. This
The overestimate due to folding and offset values is likely to be
value is determined from the RMS curve at 21.5 ± 5.5 m2 (Fig. 12).
predominant here. We base this choice on the consistency between
We tried to explain the slopes between x ∼ 200 m and x ∼ 240 m
calculations in the two first profiles (P3 and P1), and because we
by a large stepping of the fault between the two first events. The
know from numerical experiments that offset values have a strong
fit of our synthetic slope to profile P6 requires a κ�t between the
influence on age estimates (Avouac 1993).
two first events greater than 150 m2. This is inconsistent with κ�tcalculated from profiles P3 and P1 ([6.5–20] m2). Alternatively, wecould interpret the slope profile between x ∼ 200 m and x ∼ 240 m
6.2 E-W thrust scarp to the south of Baga Bogd
as the folding component of scarp morphology that has no meaning
(Figs 1 and 6)
in terms of morphological dating. Although the elevation profile P6
We stated from the previous geomorphic analysis of uplifted alluvial
looks roughly linear after x ∼ 250 m, folding seems to appear here,
fans, that this fault has not broken the surface from the deposition
although we have no direct evidence.
of the more recent surface s3 (Fig. 6). A far as we do not have
Moreover, the morphological age of the penultimate event on pro-
numerical dating of the uplifted surfaces, can we bound the age of
file P6 is much greater (21.5 ± 5.5 m2) than in the previous estimates
the last event by morphological methods?
with profiles P3 (13.5 ± 6.5 m2) and P1 (12.75 ± 6.2 m2). In orderto explain this, we suggest two possibilities: 1) the morphologic agecalculated from profiles P1 and P3 could be underestimated. Folding
6.2.1 Profile P7 (Figs 6 and 13)
tends to increase the scarp slopes and thus decrease the morpholog-ical age. 2) The estimate from profile P6 could be overestimated.
The symmetric shape suggests that rupture has remained localized
While the folding can increase the scarp slopes, it can broaden the
near the inflection point of the scarp profile. The curved trace of
part of scarp profile apparently eroded, making it older morpholog-
the fault in plan view suggests that the fault has a relatively low
ically. Therefore, offsets that we use to model the cumulative offset
dip (Fig. 6). We also have no clear indication of local incremental
of P6 may also be too high (4.25 m for P6, compared with 3.5 m
offset values, this scarp being unaffected by the 1957 earthquake.
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
S. Carretier et al.
Figure 12. Morphological dating from profile P6 (see Fig. 4 for localization). Triangles are data and solid lines are models for elevation and slope profiles. The
models correspond to four events of 4.25 m offset on faults dipping at 50◦ (see text), and successive interseismic durations of κ�t = 100, 21 and 21 m2. Using
faults 40 m, 10 m and 27 m apart to respect the location of inflections of the slope profile, the modelling suggests that the fault scarp collapsed at the time of
the third event. Consequently, we can only estimate κ�t corresponding to the last interseismic duration. Modelling suggests that it corresponds to the Gaussian
shape of the slope gradient profile. The RMS between observed (elevation) and modelled profiles is thus calculated only for this part of the elevation profile
(horizontal arrow on the elevation profile). To define the range of acceptable values of κ�t, we retain all models for which the RMS lies between RMSmin and
RMSmin +5 cm (see text for details). The first step of 40 m is a un-successful attempt to explain the slopes between 200 m and 240 m. In fact we interpret this
part of the profile to be caused by the folding component of the scarp morphology.
The morphology between x ∼ 300 m and x ∼ 400 m is controlled
by folding (Fig. 6). The cumulative offset associated with faultingis estimated at 18 m (Fig. 6).
The examples that we described illustrate a variability that depends
We postulate that incremental offsets are similar in size to those
on the balance between four processes (Bayasgalan et al. 1999a):
at Gurvan Bulag with a maximum at ∼5 m. We carried out ex-
1) surface dislocation on faults, 2) folding associated with thrust-
periments varying the incremental offset between 3 and 5 m (cor-
ing and backthrusting, 3) alluvial erosion and sedimentation, and
responding to 6 and 4 events responsible for the cumulative offset
4) slope erosion. These factors have general implications for the
of 18 m), the dip of the fixed fault between 45◦ and 90◦. We fixed
morphological dating of any transport-limited reverse fault scarps.
the value of the slope of repose at 0.7, which corresponds to theslope of the gravity-controlled face commonly observed for similar
7.1 Alluvial environment
sediments along the Gurvan Bulag scarp. Such range of parame-ters implies the total removal of the synthetic scarp after two or
Our examples suggest that cumulative reverse fault scarps can
three events, because of gravitational collapse associated with the
be dated when they are in front of drainage basins. In this case,
reverse component and the large offsets (Case A of Fig. 9). Conse-
climatically-controlled abrasion or deposition isolates surfaces that
quently, we can only date the last event from this scarp. To explain
have been uplifted by different numbers of earthquakes. This allu-
the observed smooth morphology, this scenario requires a long pe-
vial environment controls the vertical growth of forebergs whose
riod of quiescence during which the fault is inactive. We date the
morphology is dominated by slope erosion.
last event at 235 ± 39 m2 (Fig. 13). This morphological age is de-termined from the RMS versus κ�t computed over the portion of
7.2 Folding
the scarp profile presumably unaffected by folding (x ≤ 290 m,Figs 6 and 13). This tends to reduce the possible overestimate of
Folding may decrease the apparent morphological age by increas-
the morphological age due to folding, which is expressed morpho-
ing the scarp slope. It is difficult to quantify this effect. On the
logically at the upper part of the scarp. If we use the diffusion co-
other hand, if folding is masked by sedimentation, producing flat
efficient calibrated on the Gurvan Bulag Fault (which has the same
topography (e.g. profile P2, Fig. 5), we may overestimate the fault
orientation and same materials), we date the last event occurring on
offsets and therefore the morphological age of the scarp. A second
the Southern Baga thrust at 71 ± 38 ka. The uncertainty is large,
effect which can lead to an overestimate of the morphological age
but this age may correspond to the pause in surface rupture activ-
is the surface bending associated with folding, which may be mis-
ity observed in Gurvan Bulag between approximately 118 ka and
taken with diffusive-controlled morphology (e.g. Fig. 2f). The last
12 ka. The resumption of surface faulting observed along the Gurvan
two statements appear to be predominant. It is thus necessary to
Bulag scarp in the last 12 ka seems to have not occurred SE of Baga
be very cautious about what controls the cumulative offset at each
place. Sometimes analysis of natural cross-sections and of the scarp
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
Figure 13. Morphological dating from the profile P7 (see Fig. 6 for localization). The symmetric shape of the elevation profile suggests that faulting has
remained located at the inflection point of the scarp. Assuming a fault dipping at 45◦, and 4.25 m offsets, the modelling suggests that the scarp collapsed at
each event. Consequently, only the last event can be dated. The best fitting morphological age and associated uncertainty is determined graphically from the
RMS versus constant κ�t. The RMS is calculated from the elevation data, over the length corresponding to the diffusive morphology (horizontal arrow on the
elevation profile). The right part of the profile (from x ∼ 300 m) is interpreted as folding. The RMS curve refers to the last interseismic duration only. To define
the range of acceptable values of κ�t, we retain all models for which the RMS lies between RMSmin and RMSmin +5 cm (see text for details).
gradient variation helps identify folding, even if it does not appear
distributed fractures because gravitational collapse is less efficient
obviously on the scarp profile itself (profile P6, Fig. 12). Folding
at removing variations at the surface in this case (Fig. 2f ).
associated with reverse faulting could be present in all our studiedprofiles, leading in overestimated values of morphological ages. Ifso, our estimated morphological ages for large cumulative offsets
7.4 Reverse component, variable position of the main
(for which folding can affect significantly the dating) are maximum
thrust, fault offsets and gravity-driven collapse
values. These values allow to bound the age of the initiation of the
The morphology of cumulative reverse fault scarps is strongly con-
uplift, which is the aim of our study on the Gurvan Bulag fault.
trolled by gravitational collapse if faulting remains localized and
Moreover, the consistency of our results and previous estimations
if incremental vertical offsets are large (>1 m). Gravitational col-
of uplift rates and resumption of the seismic activity on the Gurvan
lapse and scarp shortening caused by the reverse component act
Bulag fault is encouraging (Ritz et al. 1999). Our study attempted
to reset the diffusive shape. If a large part of the scarp is affected
also to test the application of morphological dating method to cu-
this reduces the number of unknowns by giving a new initial state
mulative reverse faults scarps. We use a simple model to discuss the
of degradation at each event and by smoothing irregularities. On
rule of several processes. To improve further works on such scarps,
the other hand, such resetting removes information about the older
it will be necessary to add the folding in models for a more general
It is difficult to justify the use of analytical models that do not
take this reverse component and its consequent gravity-driven col-lapse into account, unless this is demonstrably unimportant in that
7.3 Distributed secondary faults
particular case. We prefer to used a forward model which, although
Trenches excavated in cumulative fault scarps can exhibit a main
simplistic, allows us to assess the importance of slope collapse by
thrust with associated secondary fractures and colluvial wedges
varying local parameters such as the slope angle of repose, the dis-
(e.g. Meghraoui et al. 1988; Philip et al. 1992). Other examples
tance between successive faults and incremental rupture offset val-
show a single fault cutting through alluvial deposits at each event
ues. Our approach helps evaluate whether a whole scarp or only
(Figs 2d,f ). Distributed faults within a scarp can cause several in-
the penultimate event can be dated. Our model is, however, lim-
flections of the scarp morphology at each seismic event. At the
ited by the value of the cumulative offset. Beyond a certain off-
same time, folding may develop with variable amplitude (e.g. Philip
set, the morphology of scarp is only controlled by folding and
& Megrhaoui 1993). When a cumulative fault scarp develops with
large incremental offsets (>1 m), the resetting effect of gravitational
A recent study pointed out that calibrated diffusivity on the shore-
collapse smooths surface irregularities and folding is only expressed
line of Lake Bonneville that non-linear diffusion matches the data
in the morphology in the upper part of the scarp. In this case, the
better than linear diffusion (Mattson & Bruhn 1999). At the scale
geomorphic evolution of a cumulative scarp is mainly controlled
of hillslopes, Roering et al. (1999) showed also that erosion is bet-
by the successive gravitational collapse after each event and dif-
ter described by non-linear erosion. Non-linear erosion effects usu-
fusive slope erosion during interseismic periods. The morphology
ally imply that the morphological ages estimated by linear diffu-
of scarps formed by small offsets is more sensitive to bending and
sion will be overestimated. We expect that these non-linear effects
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
S. Carretier et al.
remain within the uncertainties relative to erosion parameters that we
de G´eophysique, Tectonique and S´edimentologie (UMR5573) and
from the Royal Society helped with fieldwork.
7.5 Implications for the seismic behaviour of the Gurvan
R E F E R E N C E S
Bogd fault system
Andrews, D.J. & Hanks, T.C., 1985. Scarp degraded by linear diffusion:
The complexity of the interactions between structure and erosion
Inverse solution for age, J. geophys. Res., 90, 10 193–10 208.
Armijo, R., Tapponnier, P. & Tong-Lin, H., 1989. Late Cenozoic right strike-
leads only to rough morphologic ages. However, this dating method
slip faulting in southern Tibet, J. geophys. Res., 94, 2787–2838.
allows us to bound the ages of scarps, and thus to improve the cli-
Arrowsmith, J.R., Pollard, D.D. & Rhodes, D.D., 1996. Hillslope develop-
matic and thrusting histories when it is associated with other dating
ment in areas of active tectonics, J. geophys. Res., 101, 6255–6275.
methods such as cosmogenic isotope and thermoluminescence dat-
Arrowsmith, J.R., Rhodes, D.D. & Pollard, D.D., 1998. Morphologic dating
ing. On the Gurvan Bogd Range, we propose the following scenario:
of scarps formed by repeated slip events along the San Andreas Fault,
Carrizo Plain, California, J. geophys. Res., 103, 10 141–10 160.
(i) deposition of surface s1 at Pleistocene times south of Ih Bogd
Avouac, J-P, 1993. Analysis of scarp profiles: evaluation of errors in mor-
(synchronous with s1 of south Baga Bogd?);
phologic dating, J. geophys. Res., 98, 6745–6754.
(ii) thrusting of s1 and development of foreberg ridges ∼100 m
Avouac, J-P. & Peltzer, G., 1993. Active Tectonics in Southern Xinjian,
China: Analysis of Terrace Riser and Normal Fault Scarp Degradation
(iii) some time before 118 ± 7.8 ka the surficial tectonic activity
Along the Hotan-Qira Fault system, J. geophys. Res., 98, 21 773–21 807.
stops on the Gurvan Bulag thrust;
Avouac, J-P, Tapponnier, P., Bai, M., You, H. & Wang, G., 1993. Active
(iv) fluvial transport with high capacity leads to the erosion of
thrusting and folding along the Northern Tien Shan and late Cenozoicrotation of the Tarim relative to Dzungaria and Kazakhstan, J. geophys.
the scarp in front of the major drainage basin;
Res., 98, 6755–6804.
(v) deposition of surface s2 at 118 ± 17.8 ka south of Ih Bogd
Baljinnyam, I. et al., 1993. Ruptures of Major Earthquakes and Active De-
(Ritz et al. 1999);
formation in Mongolia and its Surroundings. Geol. Soc. Am., Memoir
(vi) at about 20 ka permafrost develops and then disappears at
about 14 ka (Owen et al. 1998);
Bayarsayhan, C., Bayasgalan, A., Enhtuvshin, B., Hudnut, K.W.,
(vii) deposition of surface s3 at 12.7 ± 1.95 ka, south of Ih Bogd
Kurushin, R.A., Molnar, P. &Olziybat, M., 1996. 1957 Gobi Altay Mon-
(Ritz et al. 1999);
golia earthquake as a prototype for southern California's most devastating
(viii) around 12 ka, surficial tectonic activity resumes on the
earthquake, Geology, 24, 579–582.
Gurvan Bulag thrust scarp, with four seismic events between then
Bayasgalan, A., 1999. Active teconics of Mongolia. PhD thesis, Cambridge
and the present day. The cosmogenic dating of the uplifted alluvial
Bayasgalan, A., Berryman, K., Kendrick, K., Prentice, C. & Ritz, J-F, 1997.
surface s3 allowed Ritz et al. (1999) to propose the resumption of the
Palaeoseismological investigations along the 1957 Gobi-Altay, Mongo-
seismic activity after the deposition of this surface. Our study con-
lia, Earthquake Rupture: Preliminary results from Excavations along the
firms that the Gurvan Bulag fault has been quiescent from ∼118 ka
Gurvan Bulag Thrust, EOS Trans. Am. geophys. Un., 78, 440.
to 11.7 ± 8.1 ka. This is also consistent with the date propose by
Bayasgalan, A., Jackson, J., Ritz, J-F & Carretier, S., 1999a. Forebergs,
Owen et al. (1999) for the uplift of alluvial fans (10–13 ka);
flower structures, and the development of large intra-continental strike-
(ix) earthquake of magnitude 8.3 in 1957.
slip faults: The Gurvan Bogd fault system in Mongolia, J. Struct. Geol.,
21, 1285–1302.
The apparent seismic gap observed on the Gurvan Bulag thrust
Bayasgalan, A., Jackson, J., Ritz, J-F & Carretier, S., 1999b. Field examples
between ∼118 ka and ∼12 ka may correspond to the end of seis-
of strike-slip fault terminations in Mongolia, and their tectonic signifi-
mic activity that we interpret from dating the E–W thrust scarp
cance, Tectonics, 18, 394–411.
SE of Baga Bogd (dated at 71 ± 38 ka). We thus confirm that
Ben-Zion, Y., Dahmen, K., Lyakhovsky, V., Ertas, D. & Agnon, A., 1999.
tectonic activity on the thrusts of the Gurvan Bogd Range is not
Self-driven mode switching of earthquake activity on a fault system, Earth
continuous but episodic (Ritz et al. 1999). Moreover, seismic ac-
planet. Sci. Lett., 172, 11–12.
tivity on the different thrusts of the Gurvan Bogd range is not syn-
Bevington, P.R. & Robinson, D.K., 1992. Data reduction and error analysis
for the physical sciences, 2nd ed., McGraw-hill, New-York.
chronous. Seismic activity resumes on the Gurvan Bulag thrust fault
Bierman, P.R., Gillespie, A.R. & Caffee, M.W., 1995. Cosmogenic ages for
from the early Holocene, while it stopped before on the thrust lo-
earthquake recurrence intervals and debris flow fan deposition, Owens
cated south east of Baga Bogd. This raises the general problem
Valley, California, Science, 270, 447–450.
of how distributed faults move in a regional compressive strain
Bourl es, D.L., 1992. Beryllium isotopes in the Earth's environment, Ency-
field, and how seismicity is temporally distributed on major faults
clopedia of Earth System Science, 1, 337–352.
(see for example Wesnousky 1994; Stirling et al. 1996). In the
Brown, E.T., Edmond, J.M., Raisbeck, G.M., Yiou, F., Kurz, M.D. & Brook,
Gurvan Bogd fault system, we observe a variation in fault behaviour
E.J., 1991. Examination of surface exposure ages of Antarctic moraines
with time that is seen in some palaeoseismicity studies and numer-
using in situ produced 10 Be an 26 Al, Geochim. et Cosmochim. Acta, 55,
ical models (Leonard et al. 1998; Huc et al. 1998; Ben-Zion et al.
Bucknam, R.C. & Anderson, R.E., 1978. Estimation of fault-scarp ages from
a scarp-height-slope-angle relationship, Geology, 7, 11–14.
Bull, W.B. & Pearthree, P.A., 1988. Frequency and size of quartenary sur-
face ruptures of the Pitayacachi fault, northeastern Sonora, Mexico, Bull.
seism. Soc. Am., 78, 946–978.
Carretier, S., Lucazeau, F. & Ritz, J-F, 1998. Approche num´erique des inter-
We are very grateful to R. Arrowsmith and G. Marquis for
actions entre climat, tectonique et erosion. Exemple de la faille de Bogd,
their careful reviews which improved this manuscript. We thank
Mongolie, Comptes Rendus de l'Acad´emie des Sciences, 326, 1–7.
F. Lucazeau and H. Philip for reviews and discussions. We thank also
Culling, W.E.H., 1960. Analytical theory of erosion, J. Geology, 68, 336–
J. Verdun and T. Hanks for discussions. A grant from the laboratoire
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
Enzel, Y., Amit, R., Porat, N., Zilberman, E. & Harrison, B.J., 1996. Esti-
Owen, L.A., Cunningham, W.D., Richards, B.W.M., Rhodes, E.J.,
mating the ages of fault scarps in the Arava, Israel, Tectonophysics, 253,
Windley, B.F., Dorjnamjaa, D. & Badamgarav, J., 1999. Timing of forma-
tion of forebergs in the northeastern Gobi Altai, Mongolia: implications
Florensov, N.A. & Solonenko, V.P., 1963. The Gobi Altay earthquake,
for estimating mountain uplift rates and earthquake recurrence intervals,
Akademiya Nauk USSR. Moscow.
J. Geol. Soc., Lond., 156, 457–464.
Hanks, T.C., 1999. The age of scarplike landforms from diffusion-equation
Philip, H. & Megrhaoui, M., 1993. Structural analysis and interpretation
analysis, in Quaternary geochronology, pp. 313–338, ed. Stratton Noller
of the surface deformations of the El Asnam earthquake of October 10,
J., Sowers, Lettis, AGU Washington DC.
1980, Tectonics, 2, 17–49.
Hanks, T.C. & Schwartz, D.P., 1987. Morphological dating of the pre-1983
Philip, H., Rogozhin, E., Cisternas, A., Bousquet, J-C, Borisov, B. &
fault scarp on the Lost River fault at Doublespring Pass Road, Custer
Karakhanian, A., 1992. The Armenian earthquake of 1988 December 7:
County, Idaho, Bull. seism. Soc. Am., 77, 837–846.
faulting and folding, neotectonics and palaeoseismicity, Geophys. J. Int.,
Hanks, T.C., Bucknam, R.C., Lajoie, K.R. & Wallace, R.E., 1984. Modifica-
tion of wave-cut and faulting-controlled landforms, J. geophys. Res., 89,
Ritz, J-F, Brown, E.T., Bourl es, D.L., Philip, H., Schlupp, A., Raisbeck,
G.M., Yiou, F. & Enkhtuvshin, B., 1995. Slip rates along active faults
Hanks, T.C., Ritz, J-F, Kendrick, K.J., Finkel, R.C. & Garvin, C.D., 1997. Up-
estimated with cosmic-ray-exposure dates: application to the Bogd fault,
lift rates in a continental interior: faulting offsets of a ∼100 ka abandoned
Gobi-Altai, Mongolia, Geology, 23, 1019–1022.
fan along the Bogd fault, southern Mongolia, Proc. Penrose Conference
Ritz, J-F et al., 1999. Analysing the uplift rate along the Gurvan Bulag
on the Tectonics of Continental Interiors.
thrust fault (Gobi-Altay, Mongolia) during the upper Pleistocene, EOS
Hirano, M., 1968. A mathematical model of slope developement—An ap-
Trans. Am. geophys.Un, 80, 1039.
proach to the analytical theory of erosional topography, J. Geosci., 11,
Roering, J.J., Kirchner, J.W. & Dietrich, W.E., 1999. Evidence for non-linear,
diffusive sediment transport on hillslopes and implications for landscape
Huc, M., Hassani, R. & Chery, J., 1998. Large earthquake nucleation associ-
morphology, Wat. Resour. Res., 35, 853–870.
ated with stress exchange between middle and upper crust, Geophys. Res.
Schwartz, D.P. et al., 1996. Gobi-Altay, Mongolia, palaeoseismology expe-
Lett., 25, 551–554.
dition: initial results, Eos Trans. Am.geophys. Un, 78, 462.
King, G.C.P., Stein, R.S. & Rundle, J.B., 1988. The growth of geological
Siame, L. et al., 1997. Cosmogenic dating ranging from 20 to 700 ka of a
structures by repeated earthquakes-1 Conceptual framework, J. geophys.
series of alluvial fan surfaces by the El Tigre fault, Argentina, Geology,
Res., 93, 13,307–13,318.
Kurushin, R.A., Bayasgalan, A., Olziybat, M., Enhtuvshin, B., Molnar,
Stein, R.S., King, G.C.P. & Rundle, J.B., 1988. The growth of geological
P., Bayarsayhan, C., Hudnut, K. & Lin, J., 1997. The surface rupture of
structures by repeated earthquakes—1 Field examples of continental dip-
the 1957 Gobi-Altay, Mongolia, earthquake, Spec. Pap. Geol. Soc. Am.,
slip faults, J. geophys. Res., 93, 13 319–13 331.
Vol. 320, p. 143.
Stirling, M.W., Wesnousky, S.G. & Shimazaki, K., 1996. Fault trace complex-
Leonard, G., Steinberg, D.M. & Rabinowitz, N., 1998. An indication of time-
ity, cumulative slip, and the shape of the magnitude-frequency distribution
dependant seismic behaviour-an assessment of palaeoseismic evidence
for strike-slip faults: a global survey, Geophys. J. Int., 124, 833–868.
from the Arava fault, Israel, Bull. seism. Soc. Am., 88, 767–776.
Swan, F.H., 1988. Temporal clustering of palaeoseimsic events on the Oued
Machette, M.N., 1987. Documentation of Benchmark photograph that show
Fodda fault, Algeria, Geology, 16, 1092–1095.
the effects of the 1983 Borah Peak earthquake with some considerations
Taboada, A., Bousquet, J-C & Philip, H., 1993. Coseismic elastic models of
for studies of scarp degradation, Bull. seism. Soc. Am., 77, 771–783.
folds above blind thrusts in the Betic Cordilleras (Spain) and evaluation
Mattson, A. & Bruhn, R.L., 1999. Comparison of linear and non-linear dif-
of seismic hazard, Tectonophyisics, 220, 223–241.
fusion equation models as calibrated from shoreline scarps and multiple-
Tapponnier, P. & Molnar, P., 1979. Active faulting and Cenozoic tectonics
event fault scarps: eastern Great Basin, EOS Trans. Am. geophys. Un., 80,
of the Tien Shan, Mongolian and Baykal regions, J. geophys. Res., 84,
McCalpin, P., 1996. Palaeoseismology, Academic Press Inc., New York.
Wallace, R.E., 1977. Profiles and ages of young fault scarps, north-central
Meghraoui, M., Philip, H., Albar ede, F. & Cisternas, A., 1988. Trench inves-
Nevada, GSA. Bull., 88, 1267–1281.
tigations through the trace of the 1980 El Asnam thrust Fault: Evidence
Wesnousky, S.G., 1994. The Gutenberg-Richter or Characteristic Earth-
for Palaeoseismicity, Bull. seism. Soc. Am., 78, 979–999.
quake Distribution, Which Is It?, GSA Bull., 84, 1940–1959.
Molnar, P. et al., 1994. Quaternary Climate Change and the Formation of
Yeats, R.S., Sieh, K.C. & Allen, R., 1997. The Geology of Earthquakes,
River Terraces across Growing Anticlines on the North Flank of the Tien
Oxford University press, New York.
Shan, China, J. Geology, 102, 583–602.
Nash, D.B., 1981. FAULT: a Fortran programme for modeling the deradation
of active normal fault scarps, Computers and Geosciences, 7, 249–266.
Nash, D.B., 1984. Morphological dating of fluvial terrace scarps and fault
scarps near West Yellowstone, Montana, Geol. Soc. Am. Bulletin, 95,
Nino, F., Philip, H. & Chery, J., 1998. The role of bed-parallel slip in the
Fig. A1 illustrates two important points concerning the determina-
formation of blind thrust faults, J. struct. Geol., 20, 503–516.
tion of the best fitting morphological age and its associated uncer-
Nivi ere, B., Marquis, G. & Maurin, J-C, 1998. Morphologic dating of slowly
tainty: (1) best fitting morphological age does not depend on the
evolving scarp using a diffusive analogue, Geophys. Res. Lett., 25, 2325–
assumed dip and location of faults if the distance between succes-
sive faults is large enough to preserve the morphology associated
Nivi ere, B. & Marquis, G., 2000. Evolution of terrave risers along the upper
with each interseismic period. Conversely its associated uncertainty
Rhine Graben inferred from morphologic dating methods: evidence of
depends on the dip; (2) κ�t relative to the oldest events can not be
climatic and tectonic forcing, Geophys. J. Int., 141, 577–594.
determined with good accuracy independently of the other event.
Owen, L.A., Windley, B.F., Cunningham, W.D., Badamgarav, J. &
Thus, only a mean value of κ�t can be estimated from a cumulative
Dorjnamjaa, D., 1997. Quaternary alluvial fans in the Gobi of southern
scarp profile.
Mongolia: evidence for neotectonics and climate change, J. Quatern. Sci.,
12, 239–252.
First, we want to evaluate how the morphological age depends on
Owen, L.A., Richards, B., Rhodes, E.J., Cunningham, W.D., Windley, B.F.,
the fault dip assumption. We compute a profile using non-vertical
Badamgarav, J. & Dorjnamjaa, D., 1998. Relic permafrost structures in
stepping faults and we consider it as elevation data. We compare
the Gobi of Mongolia: age and significance, J. Quatern. Sci., 13, 539–547.
then the RMS versus κ�t when assuming true dip or vertical faults.
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
S. Carretier et al.
Fig. A1(a) shows the elevation profiles and the slope profiles of these
the scarp. The distance between faults allows us to identify several
two synthetic models. The first one ("reference profile") corresponds
inflections of the slope profile corresponding to the successive sur-
to a scarp formed by four successive surface ruptures caused by a
face ruptures. The second profile ("adjusted profile") fits with the
stepping fault dipping 50◦ and three interseismic periods during
previous one, assuming that successive faults are vertical. The fitting
which diffusion is applied after gravitational collapse at the front of
of this profile is based on the analysis of the slope profile of the ref-
the scarp. The last event has not been followed by the interseismic
erence profile, as we do when we want to model real data. Fig. A1(b)
period, so that the gravity-controlled face is preserved at the front of
shows the RMS versus constant κ�t obtain for both assumptions
Figure A1. Best fitting morphological age and uncertainty determination. a) slope profile and elevation profiles for two models differing by the dip of faults.
Both models use four successive stepping faults and 3.5 offsets. The reference profile uses faults dipping at 50◦, while the adjusted profile uses vertical faults.
To obtain this profile, we adjusted the location of the vertical faults so that inflections of its slope profile corresponds with those of the reference slope profile,
as we would do when modelling real data. b) RMS versus constant κ�t when assuming true dip of faults (50◦) or incorrect vertical faults. Reference profile is
sampled at constant intervals and taken as data. The horizontal dotted lines correspond to the RMSmin +5 cm limits beneath which we consider that models
are acceptable. Both RMS curves have a minimum value at κ�t = 10 m2. However, the uncertainty of the best fitting value of κ�t is larger when assuming
incorrect vertical faults. This shows that fault dip does not affect the determination of the best fitting κ�t when morphology is preserved from collapse, but
it affects the precision of the estimate. c) RMS versus constant κ�t when assuming true dip of faults (50◦). Reference profile is taken as data. The different
RMS curves were obtained using either all interseismic durations as free parameters, or only one of them. In the second case, the other interseismic durations
are fixed at the best fitting value (κ�t = 10 m2). The horizontal line corresponds to the RMSmin +5 cm limit beneath which we consider that models are
acceptable. It shows that uncertainty grows when the parameter search procedure is applied to only one interseismic duration. In particular, the value of κ�t is
poorly resolved for the first (older) interseismic duration.
� 2002 RAS, GJI, 148, 256–277
Geophysical Journal International
Morphological dating of cumulative reverse fault scarps
(vertical and non-vertical faults). Computation of RMS is restricted
a more general parameter search, including dip and location of the
to the portion of the scarp located back to the gravity-controlled
face (for which the slope has no meaning in terms of morpholog-
Fig. A1(c) deals with the accuracy expected when determining
ical age). In order to obtain the RMS curve corresponding to the
the value of κ�t for old events. We have computed RMS curves
faults dipping at 50◦ (dashed line) we sampled the corresponding
from the reference profile, assuming correct dip of faults (50◦). We
elevation profile ("reference profile") at specified intervals and we
have incremented the value of κ�t for all events (solid line), or
incremented κ�t. The resulting RMS curve has a zero value at the
only one of them (dashed and dotted lines). In the last case, the
expected best fitting value κ�t = 10 m2. The second curve (solid
other values of κ�t are fixed at the best fitting value. The horizontal
line) corresponds to RMS values computed from "reference profile"
line corresponds to the value of minimum RMS plus 5 cm which
assuming vertical faults. This RMS curve has also a minimum value
allows to determine confidence intervals on the best fitting values.
at the best fitting κ�t = 10 m2. We define confidence intervals on
As expected, RMS curves have a zero value at the best fitting value.
the best fitting value of κ�t by considering all profiles that fit data
However, the confidence intervals are larger when varying a single
within 5 cm of minimum RMS (see horizontal lines in Fig. A1b).
κ�t. The accuracy of the estimate becomes poor if we want to
While best fitting κ�t does not depend on the assumed dip of faults,
estimate the value of κ�t associated with the oldest event (dashed
Fig. A1(b) shows that this interval is clearly greater when assuming
line, Fig. A1c). This implies that it is not possible to estimate each
incorrect dip. As far as reverse faults are usually not vertical, it is rea-
interseismic duration with a good accuracy. On the contrary, a mean
sonable to assume arbitrary dipping faults to reduce the uncertainty
value of κ�t can be determined, which leads to a mean value of the
on best fitting value. The foregoing illustrates the need to improve
morphological age of a cumulative scarp by multiplying this value
the determination of morphological ages on cumulative scarps by
by the number of interseismic periods.
� 2002 RAS, GJI, 148, 256–277
Source: https://perso-sdt.univ-brest.fr/~jacdev/pdf/carretier02.pdf
Significant Risks of Oral Why This Drug Class Should Not Be Included in a Preventive Care Mandate Rebecca Peck, M.D., C.C.D., and Charles W. Norris, M.D.* Dr. Rebecca Peck is a board-certified family physician, certified clinical densitometer, and Marquette Method NFP teacher. Dr. Peck may be
ACADÉMIE NATIONALE DE PHARMACIE SANTÉ PUBLIQUE - MÉDICAMENT - PRODUITS DE SANTÉ - BIOLOGIE - SANTÉ ET ENVIRONNEMENT Fondée le 3 août 1803 sous le nom de Société de Pharmacie de Paris Reconnue d'utilité publique le 5 octobre 1877 VEILLE SCIENTIFIQUE LETTRE n° 4 éditée sous l'égide de la Commission Prospective scientifique et Programmation








